题目内容
20.已知等比数列{an}的前n项和为2n-1,求:(1)数列{an}的通项公式;
(2)数列{an2}前n项和.
分析 (1)设等比数列{an}的前n项和为Sn=2n-1,当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1,即可得出.
(2)利用等比数列的前n项和公式即可得出.
解答 解:(1)设等比数列{an}的前n项和为Sn=2n-1,
当n=1时,a1=2-1=1;当n≥2时,an=Sn-Sn-1=(2n-1)-(2n-1-1)=2n-1.
当n=1时,上式也成立.
∴an=2n-1.
(2)${a}_{n}^{2}$=(2n-1)2=4n-1,
∴数列{an2}是等比数列,首项为1,公比为4.
∴数列{an2}前n项和=$\frac{{4}^{n}-1}{4-1}$=$\frac{1}{3}({4}^{n}-1)$.
点评 本题考查了递推关系的应用、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
11.设集合 U={1,2,3,4,5,6},A={1,2,3},B={2,5},则A∩(∁UB)=( )
| A. | {1,3 } | B. | { 2 } | C. | {2,3} | D. | { 3 } |
 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=-x2+2x.
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=-x2+2x.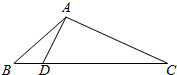 如图△ABC中,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,又己知BC边上有一点D,使∠DAC=90°,BD=$\sqrt{3}$.
如图△ABC中,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,又己知BC边上有一点D,使∠DAC=90°,BD=$\sqrt{3}$.