题目内容
1.已知f(x)=2xlnx,g(x)=-x2+ax-3.(1)求函数f(x)的最小值;
(2)若存在x∈(0,+∞),使f(x)≤g(x)成立,求实数a的取值范围.
分析 (1)函数f(x)的定义域为(0,+∞),f′(x)=2lnx+2,令f′(x)=0,解得x=$\frac{1}{e}$,再验证是否满足函数取得极小值的条件即可.
(2)存在x∈(0,+∞),使f(x)≤g(x)成立,即2xlnx≤-x2+ax-3存在x∈(0,+∞)能成立,h(x)=2lnx+x+$\frac{3}{x}$,利用导数研究其单调性极值最值即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),f′(x)=2lnx+2,令f′(x)=0,解得x=$\frac{1}{e}$,
当x∈(0,$\frac{1}{e}$)时,f′(x)<0,此时函数单调递减;当x∈($\frac{1}{e}$,+∞)时,f′(x)>0,此时函数单调递增,
故当x=$\frac{1}{e}$时,函数f(x)取得极小值即最小值为-$\frac{2}{e}$.
(2)存在x∈(0,+∞),使f(x)≤g(x)成立,
即2xlnx≤-x2+ax-3存在x∈(0,+∞)能成立?a≥2lnx+x+$\frac{3}{x}$存在x∈(0,+∞)能成立,
令h(x)=2lnx+x+$\frac{3}{x}$,则h′(x)=$\frac{(x+3)(x-1)}{{x}^{2}}$.
当x∈(0,1)时,h′(x)<0,此时函数h(x)单调递减,
当x∈(1,+∞)时,h′(x)>0,此时函数h(x)单调递增.
∴当x=1时,h(x)取得最小值4.因此a≥4,
点评 本题考查了利用导数研究函数的单调性极值与最值、存在性问题的等价转化等基础知识与基本技能方法,属于中档题

练习册系列答案
相关题目
1.已知a,b∈R,i是虚数单位,若a+i与2-bi互为共轭复数,则(a+bi)2=( )
| A. | 3-4i | B. | 3+4i | C. | 5-4i | D. | 5+4i |
13.已知复数$z=\frac{{1+2{i^3}}}{2+i}$(i为虚数单位),则z在复平面内所对应点的坐标为( )
| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (0,-1) |
11.一质点运动方程为s=2-3t2(s单位:米,t单位:秒),则此质点在1.2秒末的瞬时速度为( )
| A. | -7.2 | B. | 7.2 | C. | -2.32 | D. | 2.32 |
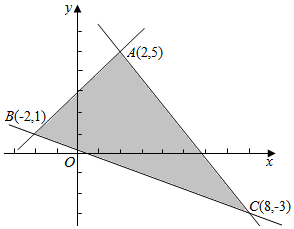 直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示:
直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示: