题目内容
半径为4的球面上有
、
、
、
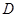四点，
、
、
两两互相垂直，则 △
、△
、△
面积和的最大值为 （ ）
| A．8 | B．16 | C．32. | D．64 |
C
解析试题分析：视AB，AC，AD为球的内接长方体的一个角，长方体的对角线即为球的直径，设它们的长分别为：a，b，c．故
，计算三个三角形的面积之和，利用基本不等式求最大值。根据题意可知，设AB=a，AC=b，AD=c，则可知AB，AC，AD为球的内接长方体的一个角．设它们的长分别为：a，b，c．故
则△、△、△面积之和的最大值为32.故选C.
考点：球体，三角形的面积公式
点评：本题考查了球内接多面体、利用基本不等式求最值问题，考查了同学们综合解决交汇性问题的能力，解答关键是利用构造法求球的直径得到a2+b2+c2=64．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
在
中，
分别是三内角
的对边,设
，则
( )
A． 或 | B． | C． | D．以上都不对 |
在
中，
，
，
，则最短边长为（ ）
A． | B． | C． | D． |
在△ABC，若
＝
＝
，则△ABC是
| A．直角三角形 | B．等腰三角形 |
| C．等腰或直角三角形 | D．钝角三角形 |
在△ABC中，a＝3，b＝
，c＝2，那么∠B等于（ ）
| A．30° | B．45° | C．60° | D．120° |
在△ABC中，角
均为锐角，且
则△ABC的形状是（ ）
| A．直角三角形 | B．锐角三角形 |
| C．钝角三角形 | D．等腰三角形 |
的内角
的对边分别为
，若
,则
等于（ ）
A． | B．2 | C． | D． |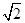
在
中,若
,
,
,则
（ ）
A． | B． | C． | D． |
在
中，已知
，
，
，P为线段AB上
的一点，且
.
，则
的最小值为( )
A． | B． | C． | D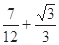． |