题目内容
在 中,若
中,若 ,
, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
B
解析试题分析:由正弦定理得: ,所以
,所以
 。
。
考点:正弦定理。
点评:正弦定理通常用来解决两种类型的问题:一是两角及一边;二是两边及其中一边的对角。在应用正弦定理来解三角形时要注意解得个数。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC的面积为
 ,则角C的度数为( )
,则角C的度数为( )
A. | B. | C. | D. |
半径为4的球面上有 、
、 、
、 、
、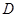 四点,
四点, 、
、 、
、 两两互相垂直,则 △
两两互相垂直,则 △ 、△
、△ 、△
、△ 面积和的最大值为 ( )
面积和的最大值为 ( )
| A.8 | B.16 | C.32. | D.64 |
在 中,
中,  ,
, ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
若DABC中,sinA:sinB:sinC = 2:3:4,那么cosC =( )
A. | B. | C. | D. |
在 中,若
中,若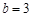 ,
, ,
, ,则
,则 的面积为( )
的面积为( )
A. | B. | C. | D. |
在 中,
中, ,
, ,其面积为
,其面积为 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
在 中,角
中,角 的对边分别为
的对边分别为 若
若 若
若 有两解,则
有两解,则 的范围是( )
的范围是( )
| A.(1,2) | B.(2,3) | C.(2, ) ) | D.(4, ) ) |
边长为5,7,8的三角形中,最大角与最小角之和为 ( )
A. | B. | C. | D. |