题目内容
在 中,已知
中,已知 ,
, ,
, ,P为线段AB上
,P为线段AB上
的一点,且 .
. ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D.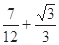 |
D
解析试题分析:因为 =
= ,sinB=cosAsinC=sin(A+C),那么利用两角和差可知sinAcosC=0,因为sinA>0,故C为直角,又因为S=
,sinB=cosAsinC=sin(A+C),那么利用两角和差可知sinAcosC=0,因为sinA>0,故C为直角,又因为S= ,那么可知tanA=
,那么可知tanA= ,那么由于点P在线段AB上,故有AC=3,BC=4,
,那么由于点P在线段AB上,故有AC=3,BC=4, ,那么利用不等式和函数性质可知
,那么利用不等式和函数性质可知 ,运用导数的思想可知最小值为
,运用导数的思想可知最小值为 ,选D.
,选D.
考点:本试题主要考查了向量的加减法几何意义以及绚丽的共线的运用。
点评:解决该试题的关键是根据三点共线,以及正弦定理和向量的数量积公式,得到边和角的函数值,进而运用函数思想求解最值。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
半径为4的球面上有 、
、 、
、 、
、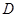 四点,
四点, 、
、 、
、 两两互相垂直,则 △
两两互相垂直,则 △ 、△
、△ 、△
、△ 面积和的最大值为 ( )
面积和的最大值为 ( )
| A.8 | B.16 | C.32. | D.64 |
在 中,
中, ,
, ,其面积为
,其面积为 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
在 中,角
中,角 的对边分别为
的对边分别为 若
若 若
若 有两解,则
有两解,则 的范围是( )
的范围是( )
| A.(1,2) | B.(2,3) | C.(2, ) ) | D.(4, ) ) |
已知 是
是 的一个内角,若
的一个内角,若 ,则
,则 是( )
是( )
| A.钝角三角形 | B.锐角三角形 |
| C.直角三角形 | D.任意三角形 |
甲船在岛B的正南方A处,AB=10千米,甲船以每小时4千米的速度向正北航行,同时乙船自B出发以每小时6千米的速度向北偏东60°的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
| A.21.5分钟 | B. 分钟 分钟 | C. 分钟 分钟 | D.2.15分钟 |
在 中,若边长和内角满足
中,若边长和内角满足 ,则角
,则角 的值是( )
的值是( )
A. | B. 或 或 | C. | D. 或 或 |
边长为5,7,8的三角形中,最大角与最小角之和为 ( )
A. | B. | C. | D. |
.在△ 中,若
中,若 ,则△
,则△ 是( )
是( )
| A.等边三角形 | B.锐角三角形 | C.钝角三角形 | D.直角三角形 |