题目内容
在△ABC中,角 均为锐角,且
均为锐角,且 则△ABC的形状是( )
则△ABC的形状是( )
| A.直角三角形 | B.锐角三角形 |
| C.钝角三角形 | D.等腰三角形 |
C
解析试题分析:∵ ∴
∴ 又角
又角 均为锐角,∴
均为锐角,∴ 为锐角,根据余弦函数在[
为锐角,根据余弦函数在[ ]单调递减,故
]单调递减,故 ,即
,即 ,所以
,所以 ,所以△ABC的形状是钝角三角形
,所以△ABC的形状是钝角三角形
考点:本题考查了三角形形状的判断
点评:判定三角形形状时,一般考虑两个方向进行变形:(1)一个方向是边,走代数变形之路,通常是正、余弦定理结合使用;(2)另一个方向是角,走三角变形之路.通常是运用正弦定理

练习册系列答案
相关题目
若 的三个内角满足
的三个内角满足 ,则
,则 ( ).
( ).
| A.一定是锐角三角形 | B.一定是直角三角形 |
| C.一定是钝角三角形 | D.可能是锐角三角形,也可能是钝角三角形 |
在 中,下列关系式不一定成立的是( )。
中,下列关系式不一定成立的是( )。
A. | B. |
C. | D. |
已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积( )
| A.9 | B.9 | C.18 | D. |
半径为4的球面上有 、
、 、
、 、
、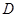 四点,
四点, 、
、 、
、 两两互相垂直,则 △
两两互相垂直,则 △ 、△
、△ 、△
、△ 面积和的最大值为 ( )
面积和的最大值为 ( )
| A.8 | B.16 | C.32. | D.64 |
若对 恒成立,则三角形ABC是( )
恒成立,则三角形ABC是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不能确定形状的三角形 |
在 中,
中,  ,
, ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
在 中,若
中,若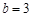 ,
, ,
, ,则
,则 的面积为( )
的面积为( )
A. | B. | C. | D. |
甲船在岛B的正南方A处,AB=10千米,甲船以每小时4千米的速度向正北航行,同时乙船自B出发以每小时6千米的速度向北偏东60°的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
| A.21.5分钟 | B. 分钟 分钟 | C. 分钟 分钟 | D.2.15分钟 |