题目内容
在
中，
分别是三内角
的对边,设
，则
( )
A． 或 | B． | C． | D．以上都不对 |
C
解析试题分析：∵，∴
又
，∴，故选C
考点：本题考查了正弦定理的运用
点评：解三角形时，由于不能唯一确定三角形的形状，因此解的情况往往不确定，可利用三角形内角和定理及“大边对大角”来判断解的情况.
练习册系列答案
小学课时特训系列答案
相关题目
在
中，若
，则
（ ）
A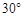． | B． | C． | D． |
在△
中，若
，则△的形状是（ ）
| A．钝角三角形 | B．直角三角形 | C．锐角三角形 | D．不能确定 |
m B．50
m 
m在△ABC中，若
，则
等于（ ）
A． | B． | C． | D． |
若
的三个内角满足
,则（ ）.
| A．一定是锐角三角形 | B．一定是直角三角形 |
| C．一定是钝角三角形 | D．可能是锐角三角形,也可能是钝角三角形 |
在△ABC中，
所对的边分别为
，则下列关系正确的是 （ ）
A． | B． |
C． | D． |
已知△ABC的面积为
,则角C的度数为( )
A． | B． | C． | D． |
半径为4的球面上有
、
、
、
四点，
、
、
两两互相垂直，则 △
、△
、△
面积和的最大值为 （ ）
| A．8 | B．16 | C．32. | D．64 |