题目内容

14．设全集U=R，集合M={x|0＜x≤1}，N={x|x≤0}，则M∩（∁UN）={x|0＜x≤1}．

分析 由题意和补集的运算求出∁UN，由交集的运算求出M∩（∁UN）．

解答 解：由N={x|x≤0}得，∁UN={x|x＞0}，
因集合M={x|0＜x≤1}，
所以M∩（∁UN）={x|0＜x≤1}，
故答案为：{x|0＜x≤1}．

点评 本题考查了交、并、补集的混合运算，属于基础题．

练习册系列答案
相关题目
4．已知椭圆C过点A（1，$\frac{3}{2}$），两个焦点为F1（-1，0），F2（1，0）．求椭圆C的方程及离心率．
5．数列{an}中，a1=1，an+1=an+2（n∈N*），求a8的值．
2．双曲线$\frac{x^2}{m+1}$+$\frac{y^2}{1-2m}$=1的焦点在y轴上，则m的取值范围是（　　）
A．m＜-1B．$-1＜m＜\frac{1}{2}$C．$m＜\frac{1}{2}$D．$m＞\frac{1}{2}$
9．设函数f（x）=-4x+2x+1-1，g（x）=lg（ax2-4x+1），若对任意x1∈R，都存在x2∈R，使f（x1）=g（x2），则实数a的取值范围为（　　）
A．（0，4]B．（-∞，4]C．（-4，0]D．[4，+∞）
19．计算题
（1）$\underset{lim}{x→0}$$\frac{{x}^{2}-2x+1}{x-1}$．
（2）$\underset{lim}{x→∞}$$\frac{2{x}^{2}-1}{1+{x}^{2}}$．
（3）$\underset{lim}{x→1}$$\frac{x-1}{\sqrt{x}-1}$．
6．在△ABC中，a，b，c分别为内角A，B，C的对边，5a2-5c2=5b2-8bc，边b，c是关于x的方程：x2-（12tanA）x+25cosA=0的两个根（b＜c），D为△ABC内任一点，点D到三边的距离和为d．
（1）求边a，b，c；
（2）求d的取值范围．
3．已知命题p：函数f（x）=$\frac{1}{3}$mx3+x2+x在区间（1，2）上单调递增；命题q：函数g（x）=4ln（x+1）+$\frac{1}{2}$x2-（m-1）x的图象上任意一点处的切线斜率恒大于1，若“p∨（￢q）”为真命题，“（￢p）∨q”也为真命题，求实数m的取值范围．
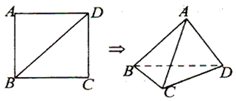
4．如图，将边长为$\sqrt{2}$的正方形ABCD沿对角线BD折起，使得AC=1，则三棱锥A-BCD的体积为（　　）
A．$\frac{{\sqrt{3}}}{6}$B．$\frac{{\sqrt{3}}}{3}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{1}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网