Question

设等差数列{a_n}的公差为d，前n项和为S_n，且a₁≥1，a₂₄≥24，S₁₂≤168，则a₉-d²的取值范围是

 

．

Answer 1

考点：等差数列的性质

专题：等差数列与等比数列,不等式的解法及应用

分析：根据等差数列的公式将不等式进行转化，利用线性规划的知识即可得到结论．

解答： 解：将a₁看成d的函数，即y=a₁，x=d，则

y≥1 y+23x≥24 y+ 11 2 x≤14

，即求y-x²+8x的范围．
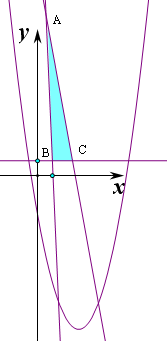
作出不等式组对应的可行域如图，
则A（

4

7

，

76

7

），B（1，1），C（

26

11

，1），
y-x²+8x为区域上的点（x，y）到C的距离，
由图象可知在B处取得最小值，yB-(12-8×1)=8，
而直线y+

11x

2

=14上能取得最大值．
M=-

11

2

x+14-(x2-8x)=-x2+

5x

2

+14，x∈(

4

7

，

26

11

)，
M的对称轴为x=

5

4

，则x∈(

4

7

，

26

11

)，
对称轴上的点能取得最大值，即Mmax=-(

5

4

)2+

5

2

×

5

4

+14=

249

16

，
∴8≤y-(x2-8x)≤

249

16

，
故答案为：[8，

249

16

]

点评：本题主要考查不等式的应用，根据等差数列的通项公式将不等式转化，利用线性规划的知识求解是解决本题的关键．综合性较强，难度较大．