题目内容
6.已知平面α的一个法向量$\overrightarrow{n}$=(3,4,-5),点A(2,-1,3),B(1,0,4),若A∈α,B∉α,则点B到平面α的距离为( )| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{2\sqrt{2}}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
分析 求出$\overrightarrow{AB}$,由点B到平面α的距离d=$\frac{|\overrightarrow{AB}•\overrightarrow{n}|}{|\overrightarrow{n}|}$,能求出结果.
解答 解:∵平面α的一个法向量$\overrightarrow{n}$=(3,4,-5),
点A(2,-1,3),B(1,0,4),A∈α,B∉α,
∴$\overrightarrow{AB}$=(-1,1,1),
点B到平面α的距离d=$\frac{|\overrightarrow{AB}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{|-3+4-5|}{\sqrt{9+16+25}}$=$\frac{2\sqrt{2}}{5}$.
故选:B.
点评 本题考查点到平面的距离的求法,是基础题,解题时要认真审题,注意向量法的合理.

练习册系列答案
相关题目
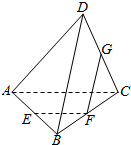 如图,在空间四边形ABCD中,E,F,G分别是AB,BC,CD的中点,
如图,在空间四边形ABCD中,E,F,G分别是AB,BC,CD的中点,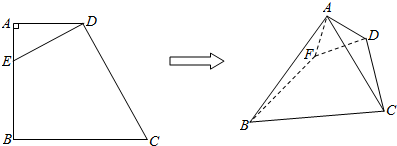
 空间四边形ABCD中,E、F分别是AB、CD的中点,AD⊥BC,且AD=4,BC=6,求异面直线EF与BC所成角的大小.
空间四边形ABCD中,E、F分别是AB、CD的中点,AD⊥BC,且AD=4,BC=6,求异面直线EF与BC所成角的大小.