题目内容
15.将半径为R的球加热,若球的半径增加△R,则球的表面积增加量△S等于4π△R(2R+△R).分析 求出半径为R时球的表面积与半径增加△R时球的表面积,计算球表面积的增加量△S值即可.
解答 解:半径为R时,球的表面积是4πR2,
当球的半径增加△R,此时球的半径为R+△R,球的表面积为4π(R+△R)2;
所以,球表面积的增加量△S=4π(R+△R)2-4πR2=4π△R(2R+△R).
故答案为:4π△R(2R+△R).
点评 本题考查了球的表面积计算公式的应用问题,也考查了变化量的计算问题,是基础题目.

练习册系列答案
相关题目
5.下列命题正确的个数是( )
①a•c=b2是a,b,c成等比数列的必要条件.
②公比q>1的等比数列的各项均大于1.
③常数列是公比为1的等比数列.
④{lg2n}}是等差数列而不是等比数列.
①a•c=b2是a,b,c成等比数列的必要条件.
②公比q>1的等比数列的各项均大于1.
③常数列是公比为1的等比数列.
④{lg2n}}是等差数列而不是等比数列.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.已知平面α的一个法向量$\overrightarrow{n}$=(3,4,-5),点A(2,-1,3),B(1,0,4),若A∈α,B∉α,则点B到平面α的距离为( )
| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{2\sqrt{2}}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
20.用二分法求方程x2=($\frac{1}{2}$)x-2的近似解时,所取的初始区间可以是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
2.甲乙两人有三个不同的学习小组A,B,C可以参加,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个小组的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
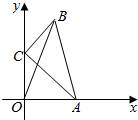 在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.
在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C随着在y轴上运动.