题目内容
1.已知函数y=f(x)是定义在R上的偶函数,当x∈(-∞,0]时,f(x)为减函数,若a=f(20.3),$b=f({{{log}_{\frac{1}{2}}}4})$,c=f(log25),则a,b,c的大小关系是( )| A. | a>b>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
分析 由题意可知f(x)在[0,+∞)为增函数,根据函数的单调性即可判断.
解答 解:函数y=f(x)是定义在R上的偶函数,当x∈(-∞,0]时,f(x)为减函数,
∴f(x)在[0,+∞)为增函数,
∵$b=f({{{log}_{\frac{1}{2}}}4})$=f(-2)=f(2),
1<20.3<2<log25,
∴c>b>a,
故选:B.
点评 考查偶函数的定义,指数函数的单调性,对于偶函数比较函数值大小的方法就是将自变量的值变到区间[0,+∞)上,根据单调性去比较函数值大小.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.已知$tan(x+\frac{π}{4})=2$,则sin2x=( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
12.函数f(x)=log3(x-1)的定义域是( )
| A. | (1,+∞) | B. | [1,+∞) | C. | {x∈R|x≠1} | D. | R |
16.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知函数f(x)=3x+4sinx-cosx的拐点是M(x0,f(x0)),则点M( )
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
6.随着“全面二孩”政策推行,我市将迎来生育高峰.今年新春伊始,宜城各医院产科就已经是一片忙碌,至今热度不减.卫生部门进行调查统计,期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中20个是“二孩”宝宝;市妇幼保健院共有30个猴宝宝降生,其中10个是“二孩”宝宝.
(I)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询.
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(Ⅱ)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(I)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询.
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(Ⅱ)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
13.已知集合A={x|x<1},B={x|x>0},则A∩B等于( )
| A. | (-∞,0) | B. | (0,1) | C. | (-∞,1) | D. | (0,+∞) |
11.某师范院校志愿者协会有10名同学,成员构成如表,其中表中部分数据不清楚,只知道从这10名同学中随机抽取一位,抽到该名同学为“中文专业”的概率为$\frac{1}{5}$.
现从这10名同学中随机选取3名同学参加社会公益活动(每位同学被选到的可能性相同)
(Ⅰ)求m,n的值;
(Ⅱ)求选出的3名同学恰为专业互不相同的概率.
(Ⅲ)设ξ为选出的3名同学中“女生”的人数,求随机变量ξ的分布列及其数学期望Eξ.
| 专业 性别 | 中文 | 英语 | 数学 | 体育 |
| 男 | m | 1 | n | 1 |
| 女 | 1 | 1 | 1 | 1 |
(Ⅰ)求m,n的值;
(Ⅱ)求选出的3名同学恰为专业互不相同的概率.
(Ⅲ)设ξ为选出的3名同学中“女生”的人数,求随机变量ξ的分布列及其数学期望Eξ.
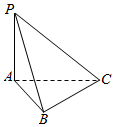 如图,已知三棱锥P-ABC中,PA⊥面ABC,PA=3,AC=4,∠ABC=90°,AB=BC.
如图,已知三棱锥P-ABC中,PA⊥面ABC,PA=3,AC=4,∠ABC=90°,AB=BC.