题目内容
数列{an}满足an=
,则该数列从第5项到第15项的和为 .
|
考点:数列的求和
专题:等差数列与等比数列
分析:设数列{2n-1}的前n项和为Sn,数列{219-n}的前n项和为Tn,由an=
,分别求出Sn,Tn,由此利用数列{an}从第5项到第15项的和S=(S10-S4)+(T15-T10),能求出结果.
|
解答:
解:设数列{2n-1}的前n项和为Sn,数列{219-n}的前n项和为Tn,
∵an=
,
Sn=
=2n-1,
Tn=
=219(1-
),
∴数列{an}从第5项到第15项的和:
S=(S10-S4)+(T15-T10)
=(210-24)+219(
-
)
=1024-16+(29-24)
=1024-16+512-16
=1504.
故答案为:1504.
∵an=
|
Sn=
| 1×(1-2n) |
| 1-2 |
Tn=
218(1-
| ||
1-
|
| 1 |
| 2n |
∴数列{an}从第5项到第15项的和:
S=(S10-S4)+(T15-T10)
=(210-24)+219(
| 1 |
| 210 |
| 1 |
| 215 |
=1024-16+(29-24)
=1024-16+512-16
=1504.
故答案为:1504.
点评:本题考查数列的前n项和的求法,是中档题,解题时要熟练掌握等比数列的前n项和的性质.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、若p∨q为真命题,则p,q均为真命题 |
| B、命题“?x0∈R,2x0≤0”的否定是“?x∈R,2x>0” |
| C、“a≥5”是“?x∈[1,2],x2-a≤0恒成立“的充要条件 |
| D、在△ABC中,“a>b”是“sinA>sinB”的必要不充分条件 |
 根据如图所示的三视图画出对应的几何体.
根据如图所示的三视图画出对应的几何体. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.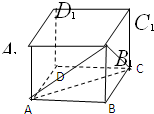 已知正方体ABCD-A1B1C1D1的棱长是a,求三棱锥B-AB1C的高.
已知正方体ABCD-A1B1C1D1的棱长是a,求三棱锥B-AB1C的高.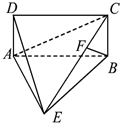 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE. 在△ABC中,∠BAC=120°,AB=
在△ABC中,∠BAC=120°,AB=