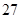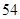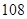题目内容
正项数列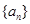 的前n项和为
的前n项和为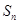 ,且
,且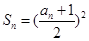 。
。
(Ⅰ)证明数列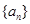 为等差数列并求其通项公式;
为等差数列并求其通项公式;
(2)设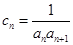 ,数列
,数列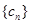 的前n项和为
的前n项和为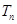 ,证明:
,证明: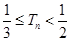 。
。
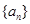 的前n项和为
的前n项和为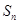 ,且
,且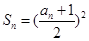 。
。(Ⅰ)证明数列
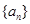 为等差数列并求其通项公式;
为等差数列并求其通项公式;(2)设
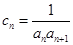 ,数列
,数列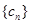 的前n项和为
的前n项和为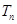 ,证明:
,证明: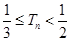 。
。(Ⅰ)详见解析,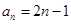 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
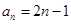 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)证明数列
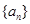 为等差数列并求其通项公式
为等差数列并求其通项公式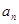 ,由已知
,由已知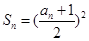 ,这是由
,这是由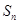 求
求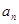 ,可根据
,可根据 来求,因此当
来求,因此当 时,
时, ,解得
,解得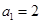 ,当
,当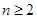 时,
时, ,整理得
,整理得 ,从而得数列
,从而得数列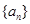 是首项为1,公差为2的等差数列,可写出数列
是首项为1,公差为2的等差数列,可写出数列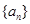 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设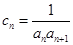 ,数列
,数列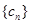 的前n项和为
的前n项和为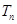 ,证明:
,证明: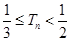 ,首先求出
,首先求出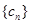 的通项公式,
的通项公式,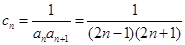 ,分母是等差数列连续两项积,符合利用拆项相消法求和,即
,分母是等差数列连续两项积,符合利用拆项相消法求和,即 ,这样求得和
,这样求得和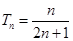 ,利用数列的单调性,可证结论.
,利用数列的单调性,可证结论.试题解析:(Ⅰ)由
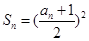 得:当
得:当 时,
时, ,得
,得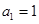 ,
,当
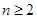 时,
时, ,
, 整理得
 ,又
,又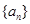 为正项数列,
为正项数列,故
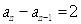 ,(
,(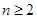 ),因此数列
),因此数列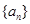 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 。(6分)
。(6分)(Ⅱ)
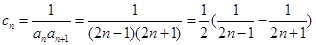 ,
,∴
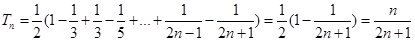 ,
,∵
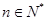 ,∴
,∴ ,(8分)
,(8分) ,
,∴数列
 是一个递增数列 ∴
是一个递增数列 ∴ ,
,综上所述,
 。(12分)
。(12分)
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 ABC中,三个内角A,B,C的对边分别为
ABC中,三个内角A,B,C的对边分别为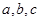 ,且A,B,C成等差数列,
,且A,B,C成等差数列,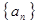 ,满足
,满足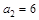 ,
,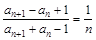
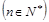 ,
, ,求数列
,求数列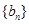 所满足的通项公式;
所满足的通项公式;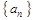 的通项公式;
的通项公式;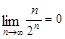 ,设
,设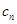 =
=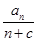
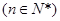 ,常数
,常数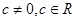 ,若数列
,若数列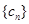 是等差数列,记
是等差数列,记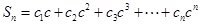 ,求
,求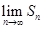 .
.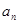 }的首项a1=1,公差d>0,且
}的首项a1=1,公差d>0,且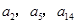 分别是等比数列{
分别是等比数列{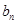 }的b2,b3,b4.
}的b2,b3,b4.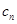 }对任意自然数n均有
}对任意自然数n均有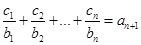 成立,求
成立,求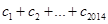 的值.
的值.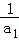 +
+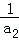 +…+
+…+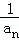 <
<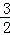 .
.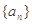 中,公差
中,公差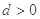 ,其前
,其前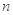 项和为
项和为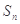 ,且满足:
,且满足: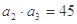 ,
,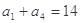 .
.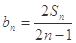 ,
,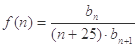 (
(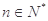 ),求
),求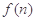 的最大值.
的最大值.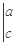
 =
=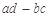 ,则
,则
 +
+
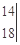 +…+
+…+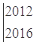
 =( )
=( )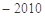
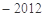
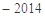

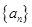 为等差数列,若
为等差数列,若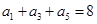 ,
,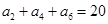 ,则公差
,则公差 .
.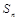 为等差数列
为等差数列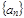 的前
的前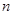 项和,
项和,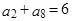 ,则
,则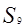 为( )
为( )