题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() .
.
(ⅰ)求函数![]() 的极小值;
的极小值;
(ⅱ)求函数![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(Ⅱ)若函数![]() 在
在![]() 上有极值,求a的取值范围.
上有极值,求a的取值范围.
【答案】(Ⅰ)(ⅰ)![]() ,(ⅱ)
,(ⅱ)![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】
(Ⅰ)(ⅰ)若![]() ,可得定义域,对其求导,令
,可得定义域,对其求导,令![]() ,得其单调性,进而求得极小值;
,得其单调性,进而求得极小值;
(ⅱ)求得![]() ,与
,与![]() 坐标,由直线的点斜式表示切线方程;
坐标,由直线的点斜式表示切线方程;
(Ⅱ)求其求导,构造![]() ,将已知
,将已知![]() 在
在![]() 上有极值,等价于
上有极值,等价于![]() 在
在![]() 上两个不等根,对方程参变分离,由不等式的简单性质得到
上两个不等根,对方程参变分离,由不等式的简单性质得到![]() 的物质范围.也可以在函数图象中利用特殊点位置与判别式求得答案.
的物质范围.也可以在函数图象中利用特殊点位置与判别式求得答案.
(Ⅰ)(ⅰ)若![]() ,则
,则![]() ,其定义域为
,其定义域为![]()
![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数有极小值![]()
(ⅱ)![]() ,
,![]() ,切线方程为
,切线方程为![]() ,即
,即![]()
(Ⅱ)由题可知,![]() .
.
法一:记![]() .
.
若![]() 在
在![]() 上有极值,等价于
上有极值,等价于![]() 在
在![]() 上两个不等根.
上两个不等根.
由![]() 得
得![]() ,
,
所以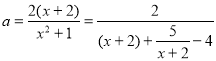 .
.
因为![]() ,所以
,所以![]() .经检验当
.经检验当![]() 时,方程
时,方程![]() 无重根.
无重根.
故函数![]() 在
在![]() 上有极值时a的取值范围为
上有极值时a的取值范围为![]() .
.
法二:![]()
若![]() 在
在![]() 上有极值,等价于
上有极值,等价于![]() 在
在![]() 上两个不等根,则
上两个不等根,则
①![]() ,
,![]()
②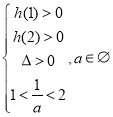
③若![]() ,得
,得![]() ,经检验不成立
,经检验不成立
④若![]() ,得
,得![]() ,经检验不成立
,经检验不成立
综上所述,a的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】为了解甲、乙两奶粉厂的产品质量,采用分层抽样的方法从甲、乙两奶粉厂生产的产品中分别抽取16件和5件,测量产品中微量元素![]() 的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
| 170 | 178 | 166 | 176 | 180 |
| 74 | 80 | 77 | 76 | 81 |
(1)已知甲厂生产的产品共有96件,求乙厂生产的产品数量;
(2)当产品中的微量元素![]() 满足
满足![]() 且
且![]() 时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
