题目内容
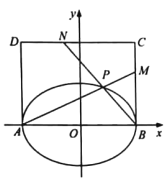
【题目】如图,在平面直角坐标系xOy中,椭圆E :![]() 的焦距为4,两条准线间的距离为8,A,B分别为椭圆E的左、右顶点.
的焦距为4,两条准线间的距离为8,A,B分别为椭圆E的左、右顶点.
(1)求椭圆E 的标准方程;
(2)已知图中四边形ABCD 是矩形,且BC=4,点M,N分别在边BC,CD上,AM与BN相交于第一象限内的点P .①若M,N分别是BC,CD的中点,证明:点P在椭圆E上;②若点P在椭圆E上,证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
【答案】(1) ![]() ;(2)①证明见解析;②证明见解析
;(2)①证明见解析;②证明见解析
【解析】
(1)由 求得
求得![]() ,进而求得椭圆的方程;
,进而求得椭圆的方程;
(2)①分别求得![]() ,
,![]() 坐标,再求得直线
坐标,再求得直线![]() 与直线
与直线![]() 方程,即可求得交点坐标,进而得证;②分别设直线
方程,即可求得交点坐标,进而得证;②分别设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,求得点
,求得点![]() ,
,![]() 坐标,则
坐标,则 ,利用斜率公式求证即可
,利用斜率公式求证即可
(1)由题, ,则
,则 ,所以
,所以![]() ,
,
所以椭圆![]() 的标准方程为:
的标准方程为:![]()
(2)证明:①由(1)可得![]() ,
,![]() ,
,
因为![]() ,且四边形
,且四边形![]() 是矩形,
是矩形,
所以![]() ,
,![]() ,
,
因为点![]() 分别是
分别是![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,
则直线![]() 为:
为:![]() ,即
,即![]() ,
,
直线![]() 为:
为:![]() ,即
,即![]() ,
,
所以 ,解得
,解得 ,即
,即
因为 ,
,
所以点![]() 在椭圆
在椭圆![]() 上
上
②设直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,
,
 ,
,
设![]()
![]() ,则
,则![]() ,
,
 ,
,
![]()

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目