题目内容
已知函数f(x)=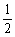 ax2-(2a+1)x+2lnx(a∈R).
ax2-(2a+1)x+2lnx(a∈R).
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)当a≤0时,求f(x)的单调区间。
解:函数f(x)的定义域为(0,+∞)
∵f ' (x)=ax-(2a+1)+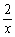
(1)由已知函数f ' (1)=f ' (3) a-(2a+1)+2=3a-(2a+1)+
a-(2a+1)+2=3a-(2a+1)+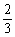
 a=
a=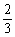
(2)f ' (x)=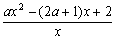 =
=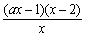 (x∈(0,+∞))
(x∈(0,+∞))
①当a=0时,f ' (x)=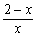 ,由f ' (x)>0得0<x<2,由f ' (x)<0得x>2
,由f ' (x)>0得0<x<2,由f ' (x)<0得x>2
∴f(x)在(0,2)上单调递增,在(2,+∞)上单调递减
②当a<0时,由f ' (x)=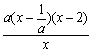 =0的x1=
=0的x1=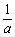 (舍去),x2=2,由f ' (x)>0的0<x<2,由f ' (x)<0的x>2
(舍去),x2=2,由f ' (x)>0的0<x<2,由f ' (x)<0的x>2
∴f(x)在(0,2)上单调递增,在(2,+∞)上单调递减
综上:当a≤0时,f(x)在(0,2)上单调递增,在(2,+∞)上单调递增

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上的函数
上的函数 的图像与
的图像与 的图像的交点为P,过点P作PP1垂直
的图像的交点为P,过点P作PP1垂直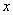 轴于点P1,直线PP1与
轴于点P1,直线PP1与 的图像交于点P2,则线段P1P2的长为________.
的图像交于点P2,则线段P1P2的长为________.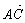 ·
·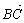 >0;条件乙:点C的坐
>0;条件乙:点C的坐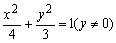 的解,则甲是乙的
的解,则甲是乙的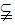 β,给出下列四个命题:
β,给出下列四个命题: 且当x∈[―3, ―2]时f(x)=4x,则f(119.5)=
且当x∈[―3, ―2]时f(x)=4x,则f(119.5)= D.-
D.- x2在x=-1处取得极大值,记g(x)=
x2在x=-1处取得极大值,记g(x)=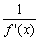 。程序框图如图所示,若输出的结果
。程序框图如图所示,若输出的结果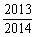 ,则判断框中可以填入的关于n的判断条件是
,则判断框中可以填入的关于n的判断条件是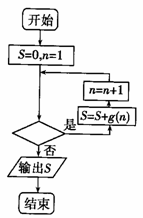
 ,则实数
,则实数 等于 ( ) A.
等于 ( ) A. B.1 C.
B.1 C. D.
D.