题目内容
正四棱锥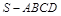 的高
的高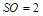 ,底边长
,底边长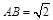 ,则异面直线
,则异面直线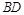 和
和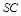 之间的距离( )
之间的距离( )
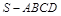 的高
的高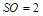 ,底边长
,底边长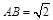 ,则异面直线
,则异面直线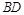 和
和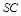 之间的距离( )
之间的距离( )A.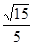 | B.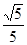 | C.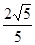 | D.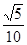 |
A
分析:连接AC,BD,证明BD⊥平面SOC,过O作OE⊥SC于E,说明OE是异面直线BD和SC之间的公垂线,OE的长度为所求,通过三角形的面积相等求出OE即可.
解答: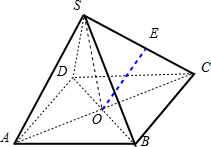 解:连接AC,BD,因为几何体是正四棱锥,所以AC⊥BD,AC∩BD=O,SO⊥底面ABCD,
解:连接AC,BD,因为几何体是正四棱锥,所以AC⊥BD,AC∩BD=O,SO⊥底面ABCD,
∴BD⊥SO,SO∩AC=O,∴BD⊥平面SOC,
过O作OE⊥SC于E,OE?平面SOC,OE⊥BD,
所以OE是异面直线BD和SC之间的公垂线,OE的长度为所求.
∵AB=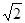 ,底面是正方形,所以AC=
,底面是正方形,所以AC=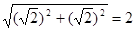 ,
,
OC=1,SO=2,所以SC=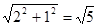 ,∴
,∴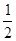 ?SO?OC=
?SO?OC=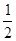 ?SC?OE,
?SC?OE,
∴OE=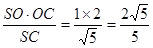 .
.
故选C.
点评:本题是中档题,考查异面直线的距离的求法,找出异面直线公垂线是解题的关键,考查空间想象能力,计算能力.
解答:
 解:连接AC,BD,因为几何体是正四棱锥,所以AC⊥BD,AC∩BD=O,SO⊥底面ABCD,
解:连接AC,BD,因为几何体是正四棱锥,所以AC⊥BD,AC∩BD=O,SO⊥底面ABCD,∴BD⊥SO,SO∩AC=O,∴BD⊥平面SOC,
过O作OE⊥SC于E,OE?平面SOC,OE⊥BD,
所以OE是异面直线BD和SC之间的公垂线,OE的长度为所求.
∵AB=
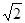 ,底面是正方形,所以AC=
,底面是正方形,所以AC=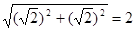 ,
,OC=1,SO=2,所以SC=
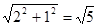 ,∴
,∴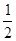 ?SO?OC=
?SO?OC=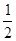 ?SC?OE,
?SC?OE,∴OE=
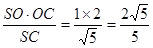 .
.故选C.
点评:本题是中档题,考查异面直线的距离的求法,找出异面直线公垂线是解题的关键,考查空间想象能力,计算能力.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
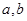 与直线
与直线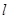 都成异面直线,则
都成异面直线,则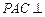 平面
平面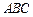 ,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO
,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO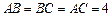 ,
,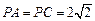 .求证:
.求证: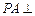 平面
平面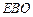 ;
;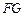 ∥平面
∥平面

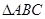 中,
中,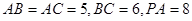 且
且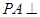 平面
平面 则
则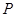 到
到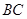 的距离为( )
的距离为( )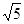
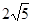
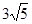
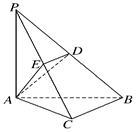 (2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;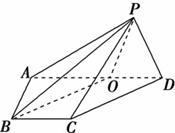
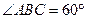 ,M是BC的中点,点N在C1C上。
,M是BC的中点,点N在C1C上。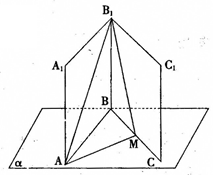
 N的位置,使
N的位置,使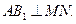
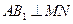 时,求二面角M—AB1—N的余弦值。
时,求二面角M—AB1—N的余弦值。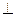 底面ABCD,PD=AD
底面ABCD,PD=AD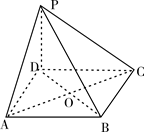
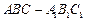 的侧棱与底面垂直,
的侧棱与底面垂直,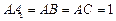 ,
,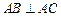 ,M是
,M是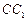 的中点,
的中点, 是
是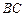 的中点,点
的中点,点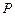 在
在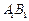 上,且满足
上,且满足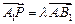 .
.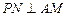 .
.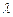 取何值时,直线
取何值时,直线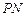 与平面
与平面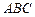 所成的角
所成的角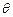 最大?并求该角最大值的正切值.
最大?并求该角最大值的正切值.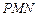 与平面
与平面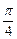 ,试确定P点的位置.
,试确定P点的位置.