题目内容
14.证明函数y=2x-5在(-∞,+∞)上是单调增函数.分析 任取x1,x2∈(-∞,+∞)且x1<x2,作差比较f(x1)和f(x2)大小可得.
解答 证明:任取x1,x2∈(-∞,+∞)且x1<x2,
记y=f(x)=2x-5,
∴f(x1)-f(x2)=(2x1-5)-(2x2-5)
=2(x1-x2)<0,即f(x1)<f(x2),
∴函数y=2x-5在(-∞,+∞)上是单调增函数.
点评 本题考查定义法证明函数的单调性,属基础题.

练习册系列答案
相关题目
2.下列各式中正确的是( )
| A. | tan735°>tan800° | B. | tan1>-tan2 | C. | tan$\frac{5π}{7}$<tan$\frac{4π}{7}$ | D. | tan$\frac{9π}{8}$<tan$\frac{π}{7}$ |
6.若抛物线y2=2mx(m>0)上的点,M(3,y0)到焦点的距离是5,则y0等于( )
| A. | 2$\sqrt{3}$ | B. | 6 | C. | ±2$\sqrt{6}$ | D. | ±$\sqrt{15}$ |
20.如果A={x|x>-1},那么下列表示正确的是( )
| A. | 0⊆A | B. | {0}∈A | C. | ∅∈A | D. | {0}⊆A |
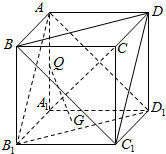 如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法:
如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法: