题目内容
【题目】在平面直角坐标系xOy中，曲线C：
经过伸缩变换
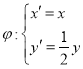后所得曲线记为
.以O为极点，x轴的正半轴为极轴，建立极坐标系Ox.
（Ⅰ）求曲线的极坐标方程；
（Ⅱ）已知A，B是曲线上任意两点，且
，求证：O到直线AB的距离为常数.
【答案】（Ⅰ）
；（Ⅱ）见解析
【解析】
（Ⅰ）由已知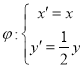
，得
，代入曲线
，即可得到曲线
的直角坐标方程，结合
，
，可得曲线的极坐标方程；
（Ⅱ）由已知
，不妨设
，
，
，
，
，由（Ⅰ）知
，
，
到直线
的距离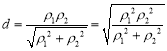
，代入即可证明到直线的距离为常数
．
解：（Ⅰ）由已知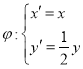
，得
，
代入C：
得
，
即曲线的直角坐标方程为：
.
又
，故极坐标方程为
，
化简得：极坐标方程为.
（Ⅱ）由已知，不妨设
，
由（Ⅰ）知：
，故
，
O到直线AB的距离
，
，
所以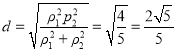
，故O到直线AB的距离为常数.
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
