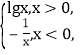题目内容
【题目】已知圆![]() 和焦点为F的抛物线
和焦点为F的抛物线![]() 上一点,M是
上一点,M是![]() 上,当点M在
上,当点M在![]() 时,
时,![]() 取得最小值,当点M在
取得最小值,当点M在![]() 时,
时,![]() 取得最大值,则
取得最大值,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据抛物线的定义和三角形中两边之差小于第三边转化![]() ,当且仅当
,当且仅当![]() 三点共线,且点N在线段
三点共线,且点N在线段![]() 上时等号成立,求得点
上时等号成立,求得点![]() 的坐标,再根据三角形中两边之差小于第三边转化
的坐标,再根据三角形中两边之差小于第三边转化![]() ,当且仅当M为线段
,当且仅当M为线段![]() 的延长线与抛物线的交点,且点N在线段
的延长线与抛物线的交点,且点N在线段![]() 上时等号成立,求得
上时等号成立,求得![]() 的坐标,从而求出
的坐标,从而求出![]() ,得解.
,得解.
由已知得:![]() ,记
,记![]() 的准线为l,如图,过点M作l的垂线,垂足为D,过点
的准线为l,如图,过点M作l的垂线,垂足为D,过点![]() 作l的垂线,垂中为
作l的垂线,垂中为![]() ,则
,则![]() ,
,
当且仅当![]() 三点共线,且点N在线段
三点共线,且点N在线段![]() 上时等号成立,此时
上时等号成立,此时![]() 取得最小值,
取得最小值,
则点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
当且仅当M为线段![]() 的延长线与抛物线的交点,且点N在线段
的延长线与抛物线的交点,且点N在线段![]() 上时等号成立,此时
上时等号成立,此时![]() 取得最大值,
取得最大值,
又直线![]() 的方程为
的方程为![]() ,由
,由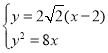 ,解得
,解得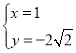 ,或
,或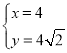 ,
,
所以![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,
,
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目