Question

曲线C₁的参数方程为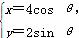 (θ为参数)，曲线C₂的极坐标方程为ρ＝2cos θ－2sin θ.

(1)化曲线C₁，C₂的方程为普通方程，并说明它们分别表示什么曲线；

(2)设曲线C₁与x轴的一个交点的坐标为P(m,0)(m>0)，经过点P作曲线C₂的切线l，求切线l的方程．

Answer 1

解：(1)曲线C₁：＋＝1，曲线C₂：(x－1)²＋(y＋1)²＝2，曲线C₁为中心为坐标原点，焦点在x轴上，长半轴长是4，短半轴长是2的椭圆；曲线C₂为圆心是(1，－1)，半径是的圆．

(2)曲线C₁：＋＝1与x轴的交点坐标为(－4,0)和(4,0)，因为m>0，

所以点P的坐标为(4,0)，显然切线l的斜率存在，设为k，则切线l的方程为y＝k(x－4)，则＝，所以7k²－6k－1＝0，得k＝1或k＝－，

所以切线l的方程为x－y－4＝0或x＋7y－4＝0.