题目内容
设二次函数f(x)=ax2+bx+c(a,b,c∈R)满足下列条件:
①当x∈R时, f(x)的最小值为0,且f(x-1)=f(-x-1)恒成立;
②当x∈(0,5)时,x≤f(x)≤2|x-1|+1恒成立.
(1)求f(1)的值;
(2)求f(x)的解析式;
(3)求最大的实数m(m>1),使得存在实数t,当x∈[1,m]时, f(x+t)≤x恒成立.
解:(1)在②中令x=1,有1≤f(1)≤1.故f(1)=1.
(2)由①知二次函数的图象关于直线x=-1对称,且开口向上,故设此二次函数为f(x)=a(x+1)2(a>0).
因为f(1)=1,所以a=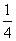 ,所以f(x)=
,所以f(x)=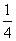 (x+1)2.
(x+1)2.
(3)f(x)=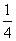 (x+1)2的图象开口向上,
(x+1)2的图象开口向上,
而y=f(x+t)的图象是由y=f(x)的图象向左或向右平移|t|个单位得到的,要在区间[1,m]上使得y=f(x+t)的图象在y=x的图象下方,且m最大,则1和m应当是方程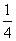 (x+t+1)2=x的两个根.
(x+t+1)2=x的两个根.
令x=1代入方程,得t=0或-4.
当t=0时,方程的解为x1=x2=1(这与m>1矛盾,舍去);
当t=-4时,方程的解为x1=1,x2=9,所以m=9.
又当t=-4时,对任意x∈[1,9],y=f(x-4)-x=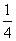 (x-3)2-x=
(x-3)2-x=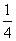 (x2-10x+9)=
(x2-10x+9)=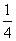 (x-5)2-4≤0,
(x-5)2-4≤0,
即f(x-4)≤x恒成立.所以最大的实数m为9.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -m,若对∀x1∈[-1,3],∃x2∈[0,2], f(x1)≥g(x2),则实数m的取值范围是________.
-m,若对∀x1∈[-1,3],∃x2∈[0,2], f(x1)≥g(x2),则实数m的取值范围是________.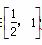 时,恒有2x≥f(x).
时,恒有2x≥f(x).


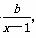 ,(a,b为常数);当3<x≤5时,y=-70x+490,已知当销售价格为2元/千克时,每日可售出该特产700千克;当销售价格为3元/千克时,每日可售出该特产150千克.
,(a,b为常数);当3<x≤5时,y=-70x+490,已知当销售价格为2元/千克时,每日可售出该特产700千克;当销售价格为3元/千克时,每日可售出该特产150千克. B.
B. C.
C. D.1
D.1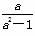 (ax-a-x)(a>0,且a≠1).
(ax-a-x)(a>0,且a≠1).