题目内容
已知函数f(x)的定义域为[0,1],且同时满足以下三个条件:①f(1)=1;②对任意的x∈[0,1],都有f(x)≥0;③当x≥0,y≥0,x+y≤1时总有f(x+y)≥f(x)+f(y).
(1)试求f(0)的值;
(2)求f(x)的最大值;
(3)证明:当x∈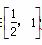 时,恒有2x≥f(x).
时,恒有2x≥f(x).
解:(1)令x∈[0,1],y=0,则有f(x)=f(x+0)≥f(x)+f(0),所以有f(0)≤0,
又根据条件②可知f(0)≥0,故f(0)=0.(也可令x=y=0)
(2)设0≤x1<x2≤1,则有f(x2)=f(x2-x1+x1)≥f(x2-x1)+f(x1)≥f(x1),即f(x)为增函数,所以f(x)≤f(1)=1,故f(x)max=1.
(3)证明:当x∈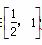 ,有2x≥1,又由(2)可知f(x)≤1,所以有2x≥f(x)对任意的x∈
,有2x≥1,又由(2)可知f(x)≤1,所以有2x≥f(x)对任意的x∈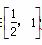 恒成立.
恒成立.

练习册系列答案
相关题目
 +
+ +
+ +…+
+…+ 的值.要求画出程序框图,写出用基本语句编写的程序.
的值.要求画出程序框图,写出用基本语句编写的程序. 的定义域是________
的定义域是________
 是奇函数.
是奇函数.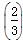 x2-x,求函数f(x)的图象在点
x2-x,求函数f(x)的图象在点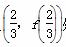 处的切线方程.
处的切线方程.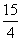 x-9都相切,求a的值.
x-9都相切,求a的值.