题目内容
在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系．圆C1，直线C2的极坐标方程分别为ρ＝4sin θ，ρcos
＝2
.
(1)求C1与C2交点的极坐标；
(2)设P为C1的圆心，Q为C1与C2交点连线的中点．已知直线PQ的参数方程为
(t∈R为参数)，求a，b的值．
解：(1)圆C1的直角坐标方程为x2＋(y－2)2＝4，
直线C2的直角坐标方程为x＋y－4＝0.
解
所以C1与C2交点的极坐标为
注：极坐标系下点的表示不惟一．
(2)由(1)可得，P点与Q点的直角坐标分别为(0,2)，(1,3)．
故直线PQ的直角坐标方程为x－y＋2＝0，
由参数方程可得y＝
x－
＋1.
所以
解得a＝－1，b＝2.
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
＋cos2x－sin2x.
π，
π]的图像(只作图不写过程)．
, 且
,
, 求
的值．
(t为参数)，以坐标原点为极点，x轴非负半轴为极轴建立极坐标系，另一直线l2的方程为ρsin θ－3ρcos θ＋4＝0，若直线l1与l2间的距离为
，则实数a的值为________．
，得到B公司面试的概率为p，且两个公司是否让其面试是相互独立的．记ξ为小王得到面试的公司个数．若ξ＝0时的概率P(ξ＝0)＝
，则随机变量ξ的数学期望E(ξ)＝________.
.
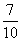B.36