题目内容
已知函数y=f(x)的定义域是[0,
),则函数y=f(sin2x)的定义域为 .
| 1 |
| 4 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由函数y=f(x)的定义域得0≤sin2x<
,利用正弦函数的性质求出x的范围,即是所求函数的定义域.
| 1 |
| 4 |
解答:
解:因为函数y=f(x)的定义域是[0,
),
所以0≤sin2x<
,解得-
<sinx<
,
则x∈(-
+2kπ,
+2kπ)∪(
+2kπ,
+2kπ)(k∈Z)
=(-
+kπ,
+kπ)(k∈Z),
故答案为:(-
+kπ,
+kπ)(k∈Z).
| 1 |
| 4 |
所以0≤sin2x<
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
则x∈(-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 7π |
| 6 |
=(-
| π |
| 6 |
| π |
| 6 |
故答案为:(-
| π |
| 6 |
| π |
| 6 |
点评:本题考查抽象函数的定义域,以及正弦函数的性质,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
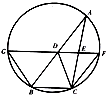 如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明: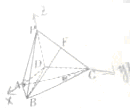 如图,在四棱锥P-ABCD中,底面ABCD是以AC为直径的圆的内接四边形,AC⊥BD,F是PC的中点,∠BAC=60°,PD⊥平面ABC.
如图,在四棱锥P-ABCD中,底面ABCD是以AC为直径的圆的内接四边形,AC⊥BD,F是PC的中点,∠BAC=60°,PD⊥平面ABC.