题目内容

函数y=n（n+4）（
2
3
）n的最大值是
 
．
考点：数列的函数特性
专题：等差数列与等比数列
分析：
f(n+1)
f(n)
=
2(n+1)(n+5)
3n(n+4)
，而分母-分子=n2-10，当n≤3时，f（n+1）＞f（n）；当n≥4时，f（n+1）＜f（n）．比较f（3），f（4），取最大值即可．
解答： 解：
f(n+1)
f(n)
=
(n+1)(n+5)(
2
3
)n+1
n(n+4)(
2
3
)n
=
2(n+1)(n+5)
3n(n+4)
，
∵分母-分子=3n2+12n-（2n2+12n+10）=n2-10，
∴当n≤3时，分母＜分子，∴f（n+1）＞f（n）；
当n≥4时，分母＞分子，∴f（n+1）＜f（n）．
而f（3）=21×(
2
3
)3=
56
9
=
504
81
，f（4）=
512
81
，
∴f（3）＜f（4）．
∴函数y=n（n+4）（
2
3
）n的最大值是
512
81
．
故答案为：
512
81
．
点评：本题考查了利用“作商法”“作差法”比较数的大小，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
已知
a
=（1，2），
b
=（1，1），且向量
a
与
a
+m
b
垂直，则m=
 
．
已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是
x=
3
2
t+m
y=
1
2
t
（t为参数）．
（1）求曲线C的直角坐标方程和直线L的普通方程；
（2）设点P（m，0），若直线L与曲线C交于A，B两点，且|PA|•|PB|=1，求实数m的值．
设
a
=（cosx，-1），
b
=（sinx-cosx，-1），函数f（x）=
a
•
b
-
1
2

（1）用五点作图法画出函数f（x）在一个周期上的图象；
（2）求函数f（x）的单调递减区间和对称中心的坐标；
（3）求不等式f（x）≥
1
2
的解集； 
（4）如何由y=
2
2
sinx的图象变换得到f（x）的图象．
在极坐标系中，已知点A（
2
，0）到直线l：ρsin（θ-
π
4
）=m（m＞0）的距离为3．
（1）求实数m值；
（2）设P是直线l上的动点，Q在线段OP上，且满足|OP||OQ|=1，求点Q轨迹方程，并指出轨迹是什么图形．
已知函数y=f（x）的定义域是[0，
1
4
），则函数y=f（sin2x）的定义域为
 
．
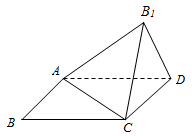已知四边形ABCD是矩形，BC=kAB（k∈R），将△ABC沿着对角线AC翻折，得到△AB1C，设顶点B1在平面ABCD上的投影为O．
（1）若点O恰好落在边AD上，
①求证：AB1⊥平面B1CD；
②若B1O=1，AB＞1．当BC取到最小值时，求k的值
（2）当k=
3
时，若点O恰好落在△ACD的内部（不包括边界），求二面角B1-AC-D的余弦值的取值范围．
在△ABC中，∠A、∠B、∠C所对的边分别是a、b、c，已知sinB=
3
5
，b=5，且∠A=2∠B，则边长a的值是
 
．
利用柯西不等式证明平方平均不等式．
设a1、a2、…，an∈R+，则
a1+a2+…+an
n
≤
a12+a22+…+an2
n
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网