题目内容
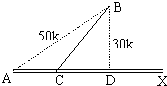
在距A城50km的B地发现稀有金属矿藏,现知由A至某方向有一条直铁路AX,B到该铁路的距离为30km,为在AB之间运送物资,拟在铁路AX上的某点C处筑一直公路通到B地.已知单位重量货物的铁路运费与运输距离成正比,比例系数为k1(k1为常数且k1>0);单位重量货物的公路运费与运输距离的平方成正比,比例系数为k2(k2为常数且k2>0).设单位重量货物的总运费为y元,AC之间的距离为xkm.
(1)将y表示成x的函数;
(2)若k1=20k2,则当x为何值时,单位重量货物的总运费最少.并求出最少运费.
(1)将y表示成x的函数;
(2)若k1=20k2,则当x为何值时,单位重量货物的总运费最少.并求出最少运费.
考点:函数模型的选择与应用
专题:函数的性质及应用
分析:(1)设AC段的运费为y1,CB段的运费为y2,然后求出两个运费,即可求出y表示成x的函数;
(2)利用k1=20k2,化简函数的表达式,利用二次函数的最值,即可求出x为何值时,单位重量货物的总运费最少.
(2)利用k1=20k2,化简函数的表达式,利用二次函数的最值,即可求出x为何值时,单位重量货物的总运费最少.
解答:
 ((10分),每小问5分)
((10分),每小问5分)
解:(1)设AC段的运费为y1,CB段的运费为y2AD=
=
=40km,
CD=AD-AC=(40-x)kmBC=
=
=
km
所以
所以y=y1+y2=k2x2+(k1-80k2)x+2500k2
(2)∵k1=20k2
∴y=k2x2-60k2x+2500k2=k2(x-30)2+1600k2
所以当x=30km时y取最小值,即ymin=y|x=30=1600k2
 ((10分),每小问5分)
((10分),每小问5分)解:(1)设AC段的运费为y1,CB段的运费为y2AD=
| AB2-BD2 |
| 502-302 |
CD=AD-AC=(40-x)kmBC=
| BD2+CD2 |
| 302+(40-x)2 |
| x2-80x+2500 |
所以
|
所以y=y1+y2=k2x2+(k1-80k2)x+2500k2
(2)∵k1=20k2
∴y=k2x2-60k2x+2500k2=k2(x-30)2+1600k2
所以当x=30km时y取最小值,即ymin=y|x=30=1600k2
点评:本题考查函数的实际应用,列出函数的解析式是解题的关键,考查分析问题解决问题的能力.

练习册系列答案
相关题目
若a是从区间[-2,2]任取的一个数,b是从区间[-2,2]任取的一个数,则关于x的一元二次方程x2+2ax-(b2-1)=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=|x2+2bx-c|(x∈R),则( )
| A、f(x)必是偶函数 |
| B、当f(-1)=f(3)时,f(x)的图象关于直线x=1对称 |
| C、若b2+c≤0,则f(x)在区间[-b,+∞)上是增函数 |
| D、f(x)有最大值|b2+c| |
若椭圆方程为
+
=1,则其焦距为( )
| x2 |
| 16 |
| y2 |
| 4 |
A、2
| ||
B、2
| ||
C、4
| ||
D、4
|
若函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<
)的图象(部分)如图所示,则( )
| π |
| 2 |

| A、A=2 | ||
B、ω=
| ||
| C、A=3 | ||
| D、ω=2 |