题目内容
如图所示，在底面是平行四边形的四棱锥P－ABCD中，点E在PD上，且PE∶ED＝2∶1，在棱PC上是否存在一点F，使BF∥平面AEC？并证明你的结论．
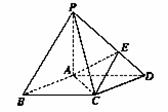
解：当F是棱PC的中点时，BF∥平面AEC，证明如下：
取PE的中点M，连接FM，则FM∥CE，①
由EM＝
PE＝ED，知E是MD的中点，设BD∩AC＝O，则O为BD的中点，连接OE，则BM∥OE，②
由①②可知，平面BFM∥平面AEC，又BF平面BFM，∴BF∥平面AEC.
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
＋
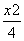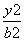＝1(0＜b＜2)的离心率为
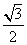，抛物线C2：x2＝2py(p＞0)的焦点是椭圆的顶点．
的展开式中的常数项为 （ ）
B．
C．
D．
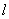是正方体的一条体对角线，点M、N、P分别为其所在棱的中点，能得出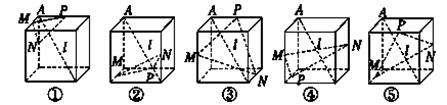
则在下列不等式：①
②
③
④
中，可以成立的不等式的个数为（ ）
的展开式的第二项的系数为
，则
的值为
B. 
C. 