题目内容
19.在△ABC中,AB=2AC=2,AD是BC边上的中线.(Ⅰ)求sin∠CAD:sin∠BAD;
(Ⅱ)若∠B=30°,求AD.
分析 (Ⅰ)由AD是BC边上的中线.可得$\frac{1}{2}AC•ADsin∠CAD$=$\frac{1}{2}$AB•ADsin∠BAD,即可解得sin∠CAD:sin∠BAD.
(Ⅱ)设BC=x,在△ABC中,由余弦定理可得:x2-2$\sqrt{3}$x+3=0,解得x=$\sqrt{3}$,由勾股定理可得AC⊥BC,可求AD的值.
解答 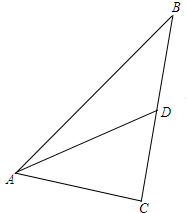 (本题满分为12分)
(本题满分为12分)
解:(Ⅰ)∵AD是BC边上的中线.
∴S△ACD=S△ABD,
∴$\frac{1}{2}AC•ADsin∠CAD$=$\frac{1}{2}$AB•ADsin∠BAD,
∴sin∠CAD:sin∠BAD=AB:AC=2:1…6分
(Ⅱ)设BC=x,在△ABC中,由余弦定理可得:AC2=BA2+BC2-2BA•BCcos∠ABC,
化简可得:x2-2$\sqrt{3}$x+3=0,
∴x=$\sqrt{3}$,
∴AC2+BC2=BA2,
∴AC⊥BC,
∴AD2=AC2+CD2=$\frac{7}{4}$,故AD=$\frac{\sqrt{7}}{2}$…12分
点评 本题主要考查了三角形面积公式,余弦定理,勾股定理在解三角形中的综合应用,考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
相关题目
10.已知函数f(x)=$\sqrt{x+3}$+$\frac{1}{x+2}$,则f(-3)=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
14.己知棱长为2的正方体ABCD-A1B1C1D1的一个面A1B1C1D1在一半球底面上,且A,B、C,D四个顶点都在此半球面上,則此半球的体积为( )
| A. | 4$\sqrt{6}$π | B. | 2$\sqrt{6}$π | C. | 16$\sqrt{3}$π | D. | 8$\sqrt{6}$π |
11.下列函数中,既是奇函数又存在零点的是( )
| A. | y=cosx | B. | y=sinx | C. | y=lnx | D. | y=$\frac{1}{x}$ |



