题目内容
15．
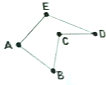如图，折五边形ABCDE中，若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯（每种颜色灯都不少于5个），每处装上一个信号灯，求使得相邻顶点所放灯的颜色不同的概率是（ ）| A． | $\frac{10}{81}$ | B． | $\frac{1}{9}$ | C． | $\frac{8}{81}$ | D． | $\frac{7}{81}$ |
分析 每处装上一个信号灯，基本事件总数n=35，由树形图得到相邻顶点所放灯的颜色不同包含的基本事件个数m=3×10=30，由此利用等可能事件概率计算公式能求出使得相邻顶点所放灯的颜色不同的概率．
解答 解：五边形ABCDE中，若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯（每种颜色灯都不少于5个），
每处装上一个信号灯，基本事件总数n=35，
相邻顶点所放灯的颜色不同，点A所放灯的颜色可以是红、黄、绿三种颜色中的一种，
当A所放灯的颜色可以是红色时，有：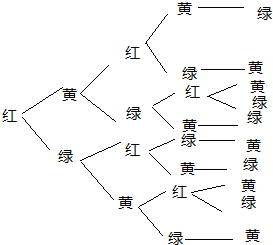
∴相邻顶点所放灯的颜色不同包含的基本事件个数m=3×10=30，
∴使得相邻顶点所放灯的颜色不同的概率p=$\frac{m}{n}$=$\frac{30}{{3}^{5}}$=$\frac{10}{81}$．
故选：A．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意树形图的合理运用．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
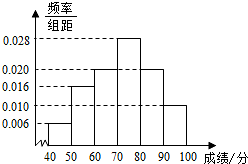新津中学高二15班学生参加“六校”联考，其数学成绩（已折合成百分制）的频率分布直方图如图所示，其中成绩分布敬意为[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]，现已知成绩落在[90，100]的有5人．