题目内容
5.直线l不经过第四象限,它的倾斜角为$\frac{π}{6}$,原点到该直线的距离为$\frac{{\sqrt{3}}}{2}$,则直线l的方程是$y=\frac{{\sqrt{3}}}{3}x+1$.分析 求出倾斜角是$\frac{π}{6}$的直线的斜率,设出直线方程,利用原点与直线的距离为$\frac{{\sqrt{3}}}{2}$,求出直线方程中的未知数,即可确定直线方程.
解答 解:因直线斜率为tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$,可设直线方程y=$\frac{\sqrt{3}}{3}$x+b,化为一般式$\frac{\sqrt{3}}{3}$x-y+b=0,
由原点到该直线的距离为$\frac{{\sqrt{3}}}{2}$,得$\frac{|b|}{\sqrt{\frac{1}{3}+1}}$=$\frac{\sqrt{3}}{2}$,解得b=±1,
∵直线l不经过第四象限,
∴b=1,
所以直线方程为$y=\frac{{\sqrt{3}}}{3}x+1$.
故答案为:$y=\frac{{\sqrt{3}}}{3}x+1$.
点评 本题考查点到直线的距离公式,考查计算能力,是基础题.

练习册系列答案
相关题目
15.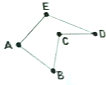 如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
 如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )| A. | $\frac{10}{81}$ | B. | $\frac{1}{9}$ | C. | $\frac{8}{81}$ | D. | $\frac{7}{81}$ |
16.从一群游戏的孩子中随机抽出k人,每人分一个苹果,让他们返回继续游戏.过一会儿,再从中任取m人,发现其中有n个孩子曾分过苹果,估计参加游戏的孩子的人数为( )
| A. | $\frac{kn}{m}$ | B. | $\frac{km}{n}$ | C. | k+m-n | D. | k+m+n |
10.关于z的方程z+i=2+iz的根是( )
| A. | $\frac{3}{2}-\frac{1}{2}$i | B. | $\frac{3}{2}+\frac{1}{2}$i | C. | 3-i | D. | 3+i |
17.函数f(x)=∫${\;}_{0}^{x}$t(t-4)dt在[-1,5]上( )
| A. | 有最大值,无最小值 | B. | 有最大值和最小值 | ||
| C. | 有最小值,无最大值 | D. | 无最值 |
14.已知向量$\overrightarrow a=(2,1),\overrightarrow b=(x,-2)$,若$\overrightarrow a$∥$\overrightarrow b$,则$\overrightarrow a+\overrightarrow b$=( )
| A. | (2,1) | B. | (-2,-1) | C. | (3,-1) | D. | (-3,1) |
15.从甲、乙、丙、丁、戊五人中任选三人作代表,这五人入选的机会均等,则甲或乙被选中的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
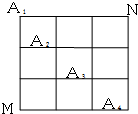 如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.