题目内容
甲、乙两个小组,甲组有3名男生2名女生,乙组有3名女生2名男生,从甲、乙两组中各选出3名同学,则选出的6人中恰有1名男生的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:求出所有的选法,求出选出的6人中恰有1名男生的选法,从而得到则选出的6人中恰有1名男生的概率
解答:
解:所有的选法共有C53•C53=10×10=100(种),则选出的6人中恰有1名男生的选法有 C31C22C33=3(种),
则选出的6人中恰有1名男生的概率等于P=
,
故选:.
则选出的6人中恰有1名男生的概率等于P=
| 3 |
| 100 |
故选:.
点评:本题考查组合数公式的应用,求随机事件的概率的方法,属于基础题

练习册系列答案
相关题目
已知,如图,三棱锥的三视图如图所示,其中俯视图是直角三角形,则这个三棱锥的体积是( )


| A、18cm3 |
| B、12cm3 |
| C、20cm3 |
| D、15cm3 |
不等式
<1的解集是( )
| x |
| |x+1| |
| A、{x|-1<x<0} |
| B、{x|x∈R,且x≠-1} |
| C、R |
| D、{x|0<x,1} |
已知变量x,y满足的不等式组
表示的是一个直角三角形围成的平面区域,则实数k=( )
|
A、-
| ||
B、
| ||
| C、0 | ||
D、0或-
|
已知△ABC的三个内角为A,B,C,且sin2C+sinAsinB=sin2A+sin2B,则角C等于( )
| A、30° | B、120° |
| C、60° | D、150° |
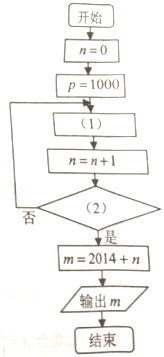 某电机厂2014年年底有资金1000万元,由于引进了先进生产设备,资金年平均增长率可达到50%,现在要设计一个程序,计算该电机厂的资金首次超过8000万元时,是哪一年的年底.
某电机厂2014年年底有资金1000万元,由于引进了先进生产设备,资金年平均增长率可达到50%,现在要设计一个程序,计算该电机厂的资金首次超过8000万元时,是哪一年的年底.