题目内容
(本小题满分13分)
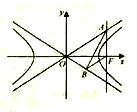
如图,已知双曲线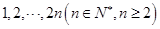 的右焦点
的右焦点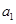 ,点
,点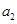 分别在
分别在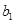 的两条渐近线上,
的两条渐近线上,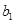 轴,
轴,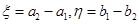 ∥
∥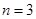 (
(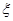 为坐标原点).
为坐标原点).
(1)求双曲线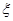 的方程;
的方程;
(2)过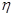 上一点
上一点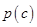 的直线
的直线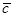 与直线
与直线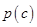 相交于点
相交于点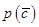 ,与直线
,与直线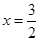 相交于点
相交于点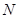 ,证明点
,证明点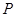 在
在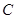 上移动时,
上移动时,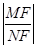 恒为定值,并求此定值.
恒为定值,并求此定值.
如图,已知双曲线
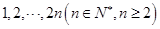 的右焦点
的右焦点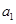 ,点
,点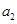 分别在
分别在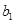 的两条渐近线上,
的两条渐近线上,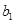 轴,
轴,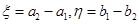 ∥
∥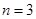 (
(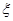 为坐标原点).
为坐标原点).
(1)求双曲线
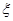 的方程;
的方程;(2)过
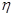 上一点
上一点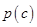 的直线
的直线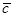 与直线
与直线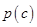 相交于点
相交于点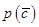 ,与直线
,与直线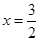 相交于点
相交于点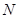 ,证明点
,证明点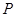 在
在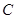 上移动时,
上移动时,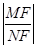 恒为定值,并求此定值.
恒为定值,并求此定值.(1) (2)
(2)
 (2)
(2)
试题分析:(1)求双曲线
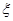 的方程就是要确定a的值,用a,c表示条件:
的方程就是要确定a的值,用a,c表示条件: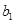 轴,
轴,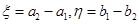 ∥
∥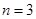 ,即可得:直线OB方程为
,即可得:直线OB方程为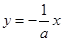 ,直线BF的方程为
,直线BF的方程为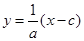 ,解得
,解得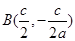 又直线OA的方程为
又直线OA的方程为 ,则
,则 又因为AB
又因为AB OB,所以
OB,所以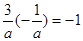 ,解得
,解得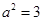 ,故双曲线C的方程为
,故双曲线C的方程为 (2)本题证明实质为计算
(2)本题证明实质为计算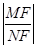 的值.分别用坐标表示直线
的值.分别用坐标表示直线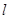 与AF的交点
与AF的交点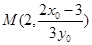 及直线
及直线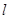 与直线
与直线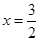 的交点为
的交点为 ,并利用
,并利用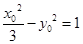 化简.:
化简.: .
.试题解析:(1)设
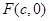 ,因为
,因为 ,所以
,所以
直线OB方程为
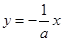 ,直线BF的方程为
,直线BF的方程为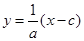 ,解得
,解得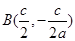
又直线OA的方程为
 ,则
,则
又因为AB
 OB,所以
OB,所以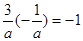 ,解得
,解得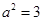 ,故双曲线C的方程为
,故双曲线C的方程为
(2)由(1)知
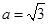 ,则直线
,则直线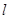 的方程为
的方程为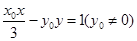 ,即
,即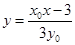
因为直线AF的方程为
 ,所以直线
,所以直线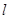 与AF的交点
与AF的交点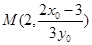
直线
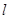 与直线
与直线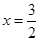 的交点为
的交点为
则
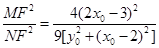
因为是C上一点,则
 ,代入上式得
,代入上式得 ,所求定值为
,所求定值为

练习册系列答案
相关题目


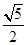
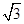
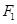 、
、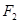 ,点A在C上,若
,点A在C上,若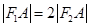 ,则
,则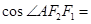 ( )
( )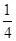
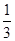
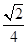
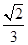
 的一条渐近线与函数
的一条渐近线与函数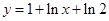 的图象相切,则双曲线
的图象相切,则双曲线 的离心率等于( )
的离心率等于( )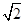

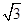


 的离心率为( )
的离心率为( )



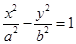 (a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( )
(a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( ) )
)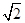 )
)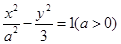 的离心率为2,则
的离心率为2,则