题目内容
椭圆C:
+
=1(a>b>0)的离心率为
,且过点(2,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=x+m与椭圆C交于两点A,B,O为坐标原点,若△OAB为直角三角形,求m的值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=x+m与椭圆C交于两点A,B,O为坐标原点,若△OAB为直角三角形,求m的值.
(Ⅰ)由已知
=
,
=1,
所以a=2,c=
,
又a2=b2+c2,所以b=1,
所以椭圆C的方程为
+y2=1;.
(Ⅱ)联立
,
消去y得5x2+8mx+4m2-4=0,△=64m2-80(m2-1)=-16m2+80,
令△>0,即-16m2+80>0,解得-
<m<
.
设A,B两点的坐标分别为(x1,y1),(x2,y2),
(ⅰ)当∠AOB为直角时,
则x1+x2=-
m,x1x2=
,
因为∠AOB为直角,所以
•
=0,即x1x2+y1y2=0,
所以2x1x2+m(x1+x2)+m2=0,
所以
-
m2+m2=0,解得m=±
.
(ⅱ)当∠OAB或∠OBA为直角时,不妨设∠OAB为直角,
由直线l的斜率为1,可得直线OA的斜率为-1,
所以
=-1,即y1=-x1,
又
+
=1;,
所以
=1;,x1=±
,m=y1-x1=-2x1=±
,
经检验,所求m值均符合题意,综上,m的值为±
和±
.
| c |
| a |
| ||
| 2 |
| 4 |
| a2 |
所以a=2,c=
| 3 |
又a2=b2+c2,所以b=1,
所以椭圆C的方程为
| x2 |
| 4 |
(Ⅱ)联立
|
消去y得5x2+8mx+4m2-4=0,△=64m2-80(m2-1)=-16m2+80,
令△>0,即-16m2+80>0,解得-
| 5 |
| 5 |
设A,B两点的坐标分别为(x1,y1),(x2,y2),
(ⅰ)当∠AOB为直角时,
则x1+x2=-
| 8 |
| 5 |
| 4m2-4 |
| 5 |
因为∠AOB为直角,所以
| OA |
| OB |
所以2x1x2+m(x1+x2)+m2=0,
所以
| 8m2-8 |
| 5 |
| 8 |
| 5 |
| 2 |
| 5 |
| 10 |
(ⅱ)当∠OAB或∠OBA为直角时,不妨设∠OAB为直角,
由直线l的斜率为1,可得直线OA的斜率为-1,
所以
| y1 |
| x1 |
又
| ||
| 4 |
| y | 21 |
所以
| 5 |
| 4 |
| x | 21 |
| 2 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
经检验,所求m值均符合题意,综上,m的值为±
| 2 |
| 5 |
| 10 |
| 4 |
| 5 |
| 5 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
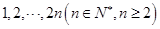 的右焦点
的右焦点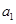 ,点
,点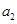 分别在
分别在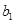 的两条渐近线上,
的两条渐近线上,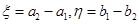 ∥
∥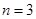 (
(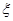 为坐标原点).
为坐标原点).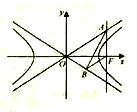
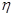 上一点
上一点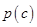 的直线
的直线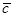 与直线
与直线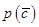 ,与直线
,与直线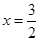 相交于点
相交于点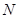 ,证明点
,证明点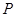 在
在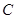 上移动时,
上移动时,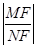 恒为定值,并求此定值.
恒为定值,并求此定值.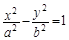 (a>0,b>0)的一条渐近线与圆
(a>0,b>0)的一条渐近线与圆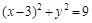 相交于A,B两点,若|AB|=2,则该双曲线的离心率为( )
相交于A,B两点,若|AB|=2,则该双曲线的离心率为( )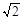
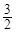
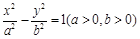 右支上的一点,满足
右支上的一点,满足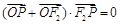 (O为坐标原点),且
(O为坐标原点),且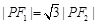 ,则该双曲线离心率为 .
,则该双曲线离心率为 . 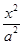 -
- =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y=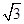 x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为________.
x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为________.