题目内容
若函数f(x)=x2+ax+b(a、b为实数,x∈R)且f(x)<4解集为(-3,1).
(1)求函数f(x)的表达式;
(2)比较x3+3x与f(x)的大小.
(1)求函数f(x)的表达式;
(2)比较x3+3x与f(x)的大小.
考点:一元二次不等式的解法,函数解析式的求解及常用方法
专题:不等式的解法及应用
分析:(1)由题意化简f(x)<4,由f(x)<4的解集与对应方程的根的关系、韦达定理求出a、b的值,代入即可求出函数f(x)的表达式;
(2)化简x3+3x-f(x)的表达式,再对x分类讨论,分别判断出各个式子的符号,从而判断出x3+3x与f(x)的大小.
(2)化简x3+3x-f(x)的表达式,再对x分类讨论,分别判断出各个式子的符号,从而判断出x3+3x与f(x)的大小.
解答:
解:(1)由f(x)=x2+ax+b得,f(x)<4为:x2+ax+b-4<0,
因为f(x)<4解集为(-3,1),所以-3、1是方程x2+ax+b-4=0的两个根,
则
,解得a=2、b=1,
所以f(x)=x2+2x+1;
(2)由(1)得,x3+3x-f(x)=x3-x2+x-1=(x-1)(x2+1),
当x>1时,(x-1)(x2+1)>0,则x3+3x>f(x);
当x=1时,(x-1)(x2+1)=0,则x3+3x=f(x);
当x<1时,(x-1)(x2+1)<0,则x3+3x<f(x).
因为f(x)<4解集为(-3,1),所以-3、1是方程x2+ax+b-4=0的两个根,
则
|
所以f(x)=x2+2x+1;
(2)由(1)得,x3+3x-f(x)=x3-x2+x-1=(x-1)(x2+1),
当x>1时,(x-1)(x2+1)>0,则x3+3x>f(x);
当x=1时,(x-1)(x2+1)=0,则x3+3x=f(x);
当x<1时,(x-1)(x2+1)<0,则x3+3x<f(x).
点评:本题考查一元二次不等式的解集与对应方程根的关系,一元二次方程根与系数关系,以及作差法比较大小,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
如果向量
=(1,2),
=(-2,0),那么
•
等于( )
| a |
| b |
| a |
| b |
| A、2 | B、-2 | C、1 | D、-1 |
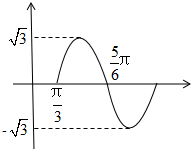 已知函数y=Asin(ωx+φ)(A>0,ω>0),一个周期内的函数图象,如图所示,求:
已知函数y=Asin(ωx+φ)(A>0,ω>0),一个周期内的函数图象,如图所示,求: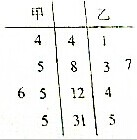 根据空气质量指数API(整数)的不同,可将空气质量分级如下表:
根据空气质量指数API(整数)的不同,可将空气质量分级如下表: