题目内容
6．如果a，b满足ab=a+b+3，那么ab的取值范围是ab≤1或ab≥9．分析 化简可得a+b=ab-3，从而可得（ab-3）2≥4ab，从而解得．
解答 解：∵ab=a+b+3，
∴a+b=ab-3，
∴（a+b）2=（ab-3）2，
∵（a+b）2≥4ab，
∴（ab-3）2≥4ab，
即（ab）2-10ab+9≥0，
故ab≤1或ab≥9；
故答案为：ab≤1或ab≥9．
点评 本题考查了学生的化简运算能力及不等式的变形应用．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
10．已知f（α）=$\frac{sin（π-α）cos（2π-α）}{sin（\frac{π}{2}+α）}$，则f（$\frac{31π}{3}$）=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
1．已知O为△ABC内一点，且有$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\overrightarrow 0$，记△ABC，△BCO，△ACO的面积分别为S1，S2，S3，则S1：S2：S3等于（ ）
| A． | 3：2：1 | B． | 3：1：2 | C． | 6：1：2 | D． | 6：2：1 |
11．△ABC中，AB=5，BC=3，CA=7，若点D满足$\overrightarrow{BD}=2\overrightarrow{DC}$，则△ABD的面积为（ ）
| A． | $\frac{{5\sqrt{3}}}{2}$ | B． | $\frac{5}{2}$ | C． | $5\sqrt{3}$ | D． | 5 |
18．已知z（2-i）=1+i，则$\overline z$=（ ）
| A． | $-\frac{1}{5}-\frac{3}{5}i$ | B． | $\frac{1}{5}+\frac{3}{5}i$ | C． | $-\frac{1}{5}+\frac{3}{5}i$ | D． | $\frac{1}{5}-\frac{3}{5}i$ |
15．将函数f（x）=sin（2x+$\frac{π}{4}$）的图象向左平移φ（φ＞0）个单位后，得到的函数图象关于y轴对称，则φ的最小值为（ ）
| A． | $\frac{5}{8}$π | B． | $\frac{3}{8}$π | C． | $\frac{π}{4}$ | D． | $\frac{π}{8}$ |
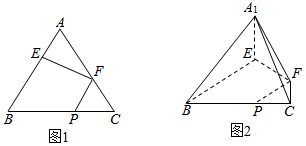在正三角形ABC中，E，F，P分别是AB，AC，BC边上的点满足AE：EB=CF：FA=CP：PB=1：2（如图1），将△AEF折起到△A1EF的位置上，连接A1B，A1C（如图2）