题目内容
5.已知圆C:x2+y2-2x-4y+m=0(1)求m的取值范围;
(2)当m=1时,若圆C与直线x+ay-2=0交于M,N两点,且CM⊥CN,求a的值.
分析 (1)把圆C的方程化为标准形式,根据半径大于零,求得m的范围.
(2)由题意可得,弦心距等于半径的$\frac{\sqrt{2}}{2}$倍,再利用点到直线的距离公式,求得a的值.
解答 解:(1)圆C:x2+y2-2x-4y+m=0,即圆C:(x-1)2+(y-2)2 =5-m,∴m<5.
(2)当m=1时,∴圆C:(x-1)2+(y-2)2 =4,
圆心C:(1,2),半径r=2,
∵CM⊥CN,∴弦心距d=$\frac{\sqrt{2}}{2}$r,即 $\frac{|1+2a-2|}{\sqrt{1+{a}^{2}}}$=$\sqrt{2}$,化简:2a2-4a-1=0,
求得a=$\frac{2±\sqrt{6}}{2}$.
点评 本题主要考查直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
13.函数f(x)=-x2+3x+a,g(x)=2x-x2,若f(g(x))≥0对x∈[0,1]恒成立,则实数a的取值范围是( )
| A. | [-e,+∞) | B. | [-ln2,+∞) | C. | [-2,+∞) | D. | (-$\frac{1}{2}$,0] |
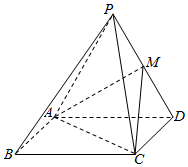 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,且△PAD是边长为4的正三角形,M为PD的中点,底面ABCD是矩形,CD=3.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,且△PAD是边长为4的正三角形,M为PD的中点,底面ABCD是矩形,CD=3.