��Ŀ����
14����֪����$f��x��=\left\{\begin{array}{l}{��{x+1}��^2}��x��0\\ \left|{{{log}_2}x}\right|��x��0\end{array}\right.$��������f��x��=a���ĸ���ͬ�Ľ�x1��x2��x3��x4����x1��x2��x3��x4����${x_3}��{{x_1}+{x_2}}��+\frac{1}{{x_3^2{x_4}}}$��ȡֵ��ΧΪ��������| A�� | ��-1��+�ޣ� | B�� | ��-1��1] | C�� | ��-�ޣ�1�� | D�� | [-1��1�� |
���� ��������f��x�����õ�x1��x2����x=-1�Գƣ�x3x4=1�������������������ν�Ͻ�����⼴�ɣ�
��� 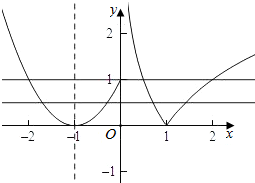 �⣺������f��x����ͼ�����ң�
�⣺������f��x����ͼ�����ң�
�߷���f��x��=a���ĸ���ͬ�Ľ�x1��x2��x3��x4����x1��x2��x3��x4��
��x1��x2����x=-1�Գƣ���x1+x2=-2��
0��x3��1��x4��
��|log2x3|=|log2x4|��
��-log2x3=log2x4��
��log2x3+log2x4=0
��log2x3x4=0
��x3x4=1��
��|log2x|=1��x=2��$\frac{1}{2}$��
��1��x4��2��$\frac{1}{2}$��x3��1��
��${x_3}��{{x_1}+{x_2}}��+\frac{1}{{x_3^2{x_4}}}$=-2x3+$\frac{1}{{x}_{3}}$��$\frac{1}{2}$��x3��1��
����y=-2x3+$\frac{1}{{x}_{3}}$����$\frac{1}{2}$��x3��1����������
���x3=$\frac{1}{2}$ȡ�����ֵ��Ϊy=1��
��x3=1ʱ������ֵΪ-1��
������ȡֵ��Χ�ǣ�-1��1]��
��ѡ��B
���� ���⿼��ֶκ��������ã���Ҫ���麯���ĵ����Ե����ã��������ν�ϵ�˼�뷽���ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
2��˫����$\frac{{y}^{2}}{4}$-x2=1��һ�������ߵķ���Ϊ��������
| A�� | y=2x | B�� | y=4x | C�� | y=$\frac{1}{2}$x | D�� | y=$\frac{1}{4}$x |
9����x��y����Լ������$\left\{\begin{array}{l}{x-y��0}\\{x+2y-6��0}\\{2x+y-3��0}\end{array}\right.$��Ŀ�꺯��z=ax-y���ڣ�0��3��ȡ�����ֵ����a��ȡֵ��Χ�ǣ�������
| A�� | ��$\frac{1}{2}$��+�ޣ� | B�� | ��-2��-$\frac{1}{2}$�� | C�� | ��-�ޣ�-$\frac{1}{2}$�� | D�� | ��-�ޣ�-2�� |
19��ֱ��5x-12y+8=0��Բx2+y2-2x=0��λ�ù�ϵ�ǣ�������
| A�� | ���� | B�� | �ཻ | C�� | ���� | D�� | ���ж� |
4�����ռ�����$\overrightarrow{a}$=��1��-2��1����$\overrightarrow{b}$=��1��0��2������������������Ϊ����$\overrightarrow{a}$��$\overrightarrow{b}$����ƽ���һ�����������ǣ�������
| A�� | ��4��-1��2�� | B�� | ��-4��-1��2�� | C�� | ��-4��1��2�� | D�� | ��4��-1��-2�� |