题目内容
(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)
设 是角
是角 的终边上任意一点,其中
的终边上任意一点,其中 ,
, ,并记
,并记 .若定义
.若定义 ,
, ,
, .
.
(Ⅰ)求证 是一个定值,并求出这个定值;
是一个定值,并求出这个定值;
(Ⅱ)求函数 的最小值.
的最小值.
(1)定值为3;(2) ;
;
【解析】
试题分析:(1)由题可知,分别将6个三角函数分别代入,进行简单的化简,即可得到定值3;(2)将 中的未知量均用
中的未知量均用 来表示,得到
来表示,得到 ,运用换元法设
,运用换元法设 ,化简成
,化简成 ,再利用均值不等式即可得到最值。
,再利用均值不等式即可得到最值。
试题解析:(Ⅰ)
 ;
;
(Ⅱ)由条件, ,
, ,
,
令

 令
令 ,
,
则
 ,
, ,且
,且 ,
,
从而


 ,令
,令 ,则
,则 ,
, ,且
,且 ,
, .所以,
.所以, .
.
从而 ,即
,即 .
.
考点:①任意角的三角函数定义②均值不等式的应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,用二分法求方程
,用二分法求方程 内近似解的过程中得
内近似解的过程中得 则方程的根落在区间 (填区间)
则方程的根落在区间 (填区间) ,则
,则 ______.
______.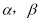 表示不重合的两个平面,
表示不重合的两个平面,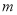 ,
,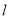 表示不重合的两条直线.若
表示不重合的两条直线.若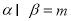 ,
,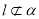 ,
,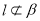 ,则“
,则“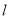 ∥
∥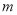 ”是“
”是“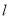 ∥
∥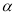 且
且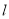 ∥
∥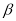 ”的( )
”的( ) 满足
满足 ,且
,且 ,求:
,求: 的解析式;
的解析式; 在
在 上的值域.
上的值域. 时,
时, 均有意义,则函数
均有意义,则函数 的图像大致是( )
的图像大致是( )
 表示的平面区域的面积为________.
表示的平面区域的面积为________.