题目内容
已知从一点P引出三条射线PA、PB、PC,且两两成角60°,则二面角A-PB-C的余弦值是( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点:二面角的平面角及求法
专题:空间角
分析:在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,连接AC在△ACM中,作AN垂直于CM于点N,∠AMN就是二面角A-PB-C的平面角,解三角形AMN,即可得到二面角A-PB-C的余弦.
解答:
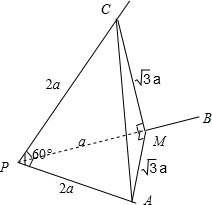 解:在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,连接AC,
解:在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,连接AC,
由图看出,在直角△PAM中,∠APM=60°,
令PM=a,则AP=2a AM=
a 同样,在直角△PCM中,∠CPM=60°,
令PM=a,则CP=2a CM=
由于∠APC=60°,PA=PC=2a
所以△PAC为等边三角形,AC=2a
在△ACM中,作AN垂直于CM于点N,
令MN=b,CN=
a-b,AN=x,
由勾股定理,△AMN中 (
a)2-x2=b2
△ACN中 (2a)2-x2=(
a-b)2联合两式消去x整理的,
a=
b 即
=
,
=
所以 cosM=
=
∴二面角A-PB-C的余弦值是
.
故选:A.
 解:在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,连接AC,
解:在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,连接AC,由图看出,在直角△PAM中,∠APM=60°,
令PM=a,则AP=2a AM=
| 3 |
令PM=a,则CP=2a CM=
| 3 |
所以△PAC为等边三角形,AC=2a
在△ACM中,作AN垂直于CM于点N,
令MN=b,CN=
| 3 |
由勾股定理,△AMN中 (
| 3 |
△ACN中 (2a)2-x2=(
| 3 |
a=
| 3 |
| b |
| a |
| ||
| 3 |
| b | ||
|
| 1 |
| 3 |
所以 cosM=
| b | ||
|
| 1 |
| 3 |
∴二面角A-PB-C的余弦值是
| 1 |
| 3 |
故选:A.
点评:本题考查的知识点是二面角的平面角及求法,其中求出二面角的平面角是解答本题的关键.

练习册系列答案
相关题目
下列函数为奇函数,且在(-∞,0)上单调递减的函数是( )
| A、f(x)=-x2 |
| B、f(x)=x-1 |
| C、f(x)=x |
| D、f(x)=x3 |