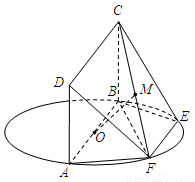
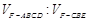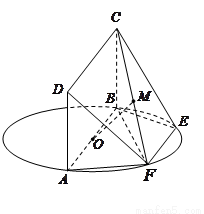题目内容
如图,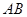 为圆
为圆 的直径,点
的直径,点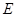 、
、 在圆
在圆 上,
上, ,矩形
,矩形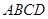 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
,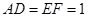 .
.

(1)求证: 平面
平面 ;
;
(2)设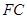 的中点为
的中点为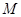 ,求证:
,求证: 平面
平面 ;
;
(3)设平面 将几何体
将几何体 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为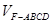 ,
, ,求
,求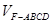
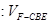 .
.
【答案】
(1)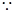 平面
平面 平面
平面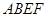 ,
,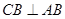 ,
, 平面
平面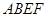
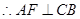 又
又 为圆
为圆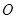 的直径,
的直径,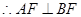
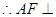 平面
平面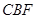 (2)设
(2)设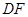 的中点为
的中点为 ,则
,则
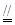
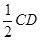 ,又
,又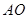
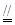
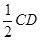 ,则
,则
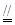
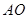 ,
,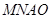 为平行四边形
为平行四边形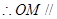
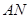 ,
,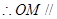 平面
平面 (3)
(3)
【解析】
试题分析:(1)证明:
 平面
平面 平面
平面 ,
,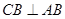 ,
,
平面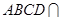 平面
平面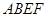 =
=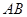 ,
, 平面
平面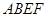 ,
,
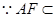 平面
平面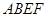 ,
,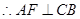 , 2分
, 2分
又 为圆
为圆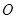 的直径,
的直径,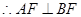 ,
,
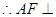 平面
平面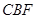 。 4分
。 4分
(2)设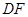 的中点为
的中点为 ,则
,则
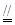
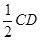 ,又
,又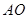
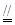
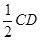 ,
,
则
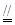
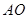 ,
,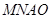 为平行四边形, 6分
为平行四边形, 6分
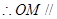
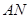 ,又
,又 平面
平面 ,
,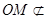 平面
平面 ,
,
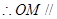 平面
平面 。 9分
。 9分
(3)过点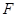 作
作 于
于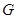 ,
,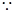 平面
平面 平面
平面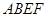 ,
,
 平面
平面 ,
,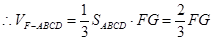 , 10分
, 10分
 平面
平面 ,
,
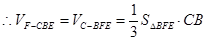
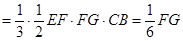 , 12分
, 12分
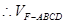
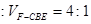 . 14分
. 14分
考点:线面垂直平行的判定及椎体的体积
点评:根据椎体的体积公式 ,求体积比主要是找到底面积和高的关系,判定线面垂直要判定直线垂直于平面内的两条相交直线,判定线面平行可转化为面外直线平行于面内直线或由两面平行得其中一面内直线平行于另外一面
,求体积比主要是找到底面积和高的关系,判定线面垂直要判定直线垂直于平面内的两条相交直线,判定线面平行可转化为面外直线平行于面内直线或由两面平行得其中一面内直线平行于另外一面

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,
如图, 为圆
为圆 的直径,点
的直径,点 、
、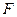 在圆
在圆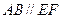 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 ,
, .
. 求证:
求证: 平面
平面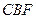 ;
;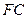 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
; 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为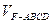 ,
,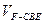 ,求
,求 .
.
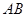 为圆
为圆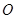 的直径,点
的直径,点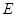 、
、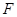 在圆
在圆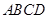 所在的平面和圆
所在的平面和圆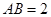 ,
,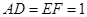 .
.
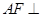 平面
平面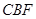 ;
;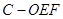 的体积.
的体积.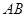 为圆
为圆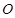 的直径,点
的直径,点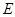 、
、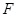 在圆
在圆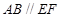 ,矩形
,矩形 的边
的边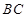 垂直于圆
垂直于圆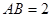 ,
,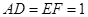 .
.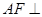 平面
平面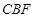 ;
; 的中点为
的中点为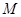 ,求证:
,求证: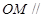 平面
平面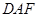 ;
;
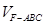 .
.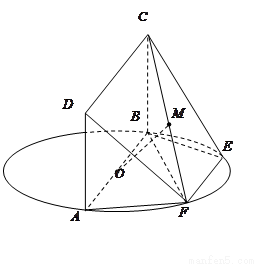
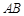 为圆
为圆 的直径,点
的直径,点 、
、 在圆
在圆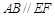 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 ,
, .
. 平面
平面 ;
; 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;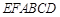 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为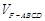 ,
, ,
,