题目内容
9.已知($\frac{4}{x}-\sqrt{\frac{x}{2}}$)9的展开式中x3的系数为$\frac{9}{4}$.分析 写出二项展开式的通项,由x得指数为3求得r值,则答案可求.
解答 解:由${T}_{r+1}={C}_{9}^{r}(\frac{4}{x})^{9-r}(-\sqrt{\frac{x}{2}})^{r}$=$(-1)^{r}{2}^{18-\frac{5}{2}r}{C}_{9}^{r}{x}^{\frac{3}{2}r-9}$,
令$\frac{3}{2}r-9=3$,得r=8,
∴展开式中x3的系数为$(-1)^{8}×{2}^{-2}×{C}_{9}^{8}=\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查二项式系数的性质,关键是对通项公式的记忆与应用,是基础题.

练习册系列答案
相关题目
20.若复数(1-ai)2(i为虚数单位,a∈R)是纯虚数,则a=( )
| A. | 1 | B. | -1 | C. | 0 | D. | ±1 |
19.已知数列{an}的前n项和为Sn(Sn≠0),a1=$\frac{1}{2}$,且对任意正整数n,都有an+1+SnSn+1=0,则a1+a20=( )
| A. | $\frac{209}{420}$ | B. | $\frac{19}{21}$ | C. | $\frac{23}{42}$ | D. | $\frac{13}{42}$ |
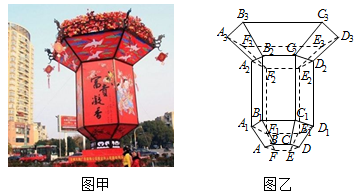 某地为了庆祝国庆66周年,现计划在城市中心广场搭建一个巨型花篮(如图甲).其中主体框梨(如图乙)准备用钢材焊接而成,具体设计方案如下:①上、中、下三部分依次由正六棱台、正六棱柱、正六棱台组成;②这三个几何体的侧面用于张贴宣传城市风光的图片,且侧面积之和为108m2;③BC:B1C1:B3C3=1:2:4,∠BB1C1=∠B2B3C3=α,且sinα=$\frac{4}{5}$,设BC=xm,B1B2=ym.
某地为了庆祝国庆66周年,现计划在城市中心广场搭建一个巨型花篮(如图甲).其中主体框梨(如图乙)准备用钢材焊接而成,具体设计方案如下:①上、中、下三部分依次由正六棱台、正六棱柱、正六棱台组成;②这三个几何体的侧面用于张贴宣传城市风光的图片,且侧面积之和为108m2;③BC:B1C1:B3C3=1:2:4,∠BB1C1=∠B2B3C3=α,且sinα=$\frac{4}{5}$,设BC=xm,B1B2=ym.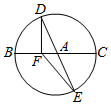 如图,BC是半径为3的圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=2$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值为( )
如图,BC是半径为3的圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=2$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值为( ) 如图,有一块荒地,形状为一个角,把这个角记为∠A(角的两边足够长),经测量∠A=120°,现在分别在∠A的两边选取P,Q两点,且PQ=200米.
如图,有一块荒地,形状为一个角,把这个角记为∠A(角的两边足够长),经测量∠A=120°,现在分别在∠A的两边选取P,Q两点,且PQ=200米.