题目内容
8.在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2b-c)cosA=acosC.(])求角A的大小;
(2)设$\overrightarrow{m}$=(0,-1),$\overrightarrow{n}$=(cosB,2cos2$\frac{C}{2}$).试求|$\overrightarrow{m}$+$\overrightarrow{n}$|的最小值.
分析 (1)根据正弦定理便可由(2b-c)cosA=acosC得,(2sinB-sinC)cosA=sinAcosC,由两角和的正弦公式便可得到2sinBcosA=sinB,从而得出$cosA=\frac{1}{2}$,这便得出$A=\frac{π}{3}$;
(2)先得出$\overrightarrow{m}+\overrightarrow{n}=(cosB,cosC)$,从而得出$|\overrightarrow{m}+\overrightarrow{n}|=\sqrt{co{s}^{2}B+co{s}^{2}C}$=$\sqrt{1+\frac{1}{2}(cos2B+cos2C)}$,带入2B=(B+C)+(B-C),2C=(B+C)-(B-C),利用两角和差的余弦公式便可以化简成$|\overrightarrow{m}+\overrightarrow{n}|=\sqrt{1-\frac{1}{2}cos(B-C)}$,从而看出B=C时,$|\overrightarrow{m}+\overrightarrow{n}|$取到最小值,并可求出该最小值.
解答 解:(1)根据正弦定理,b=2rsinB,c=2rsinC,a=2rsinA,带入(2b-c)cosA=acosC得:
(4rsinB-2rsinC)cosA=2rsinAcosC;
∴(2sinB-sinC)cosA=sinAcosC;
∴2sinBcosA=sinAcosC+cosAsinC=sin(A+C)=sinB;
∴$cosA=\frac{1}{2}$;
∴$A=\frac{π}{3}$;
(2)$2co{s}^{2}\frac{C}{2}=1+cosC$;
∴$\overrightarrow{n}=(cosB,1+cosC)$;
∴$\overrightarrow{m}+\overrightarrow{n}=(cosB,cosC)$;
∴$|\overrightarrow{m}+\overrightarrow{n}|=\sqrt{co{s}^{2}B+co{s}^{2}C}$
=$\sqrt{\frac{1+cos2B}{2}+\frac{1+cos2C}{2}}$
=$\sqrt{1+\frac{1}{2}(cos2B+cos2C)}$
=$\sqrt{1+\frac{1}{2}[cos(B+C)cos(B-C)-sin(B+C)sin(B-C)+cos(B+C)cos(B-C)+sin(B+C)sin(B-C)]}$
=$\sqrt{1+cos\frac{2π}{3}cos(B-C)}$
=$\sqrt{1-\frac{1}{2}cos(B-C)}$;
∴cos(B-C)=1,即B=C时,$|\overrightarrow{m}+\overrightarrow{n}|$取最小值$\frac{\sqrt{2}}{2}$.
点评 考查正弦定理,以及两角和差的正余弦公式,二倍角的余弦公式,三角形的内角和为π.

| A. | $\frac{1}{12}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{9}$ | D. | $\frac{2}{3}$ |
| A. | 1 | B. | -1 | C. | 0 | D. | ±1 |
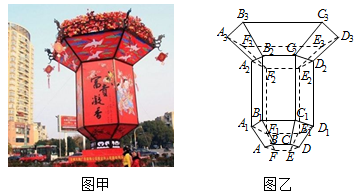 某地为了庆祝国庆66周年,现计划在城市中心广场搭建一个巨型花篮(如图甲).其中主体框梨(如图乙)准备用钢材焊接而成,具体设计方案如下:①上、中、下三部分依次由正六棱台、正六棱柱、正六棱台组成;②这三个几何体的侧面用于张贴宣传城市风光的图片,且侧面积之和为108m2;③BC:B1C1:B3C3=1:2:4,∠BB1C1=∠B2B3C3=α,且sinα=$\frac{4}{5}$,设BC=xm,B1B2=ym.
某地为了庆祝国庆66周年,现计划在城市中心广场搭建一个巨型花篮(如图甲).其中主体框梨(如图乙)准备用钢材焊接而成,具体设计方案如下:①上、中、下三部分依次由正六棱台、正六棱柱、正六棱台组成;②这三个几何体的侧面用于张贴宣传城市风光的图片,且侧面积之和为108m2;③BC:B1C1:B3C3=1:2:4,∠BB1C1=∠B2B3C3=α,且sinα=$\frac{4}{5}$,设BC=xm,B1B2=ym.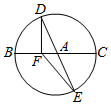 如图,BC是半径为3的圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=2$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值为( )
如图,BC是半径为3的圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=2$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值为( )