题目内容
选修4-1:几何证明选讲(本小题满分10分)
如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.

(1)求AC的长;
(2)求证:BE = EF.
【解析】
(1)∵PA2=PCPD,PA=2,PC=1,∴PD=4,
又∵PC=ED=1,∴CE=2,
∵∠PAC=∠CBA,∠PCA=∠CAB,
∴△PAC∽△CBA,∴
∴AC2=PCAB=2,∴AC= (5分)
(5分)
(2)∵BE=AC= ,CE=2,而CEED=BEEF,
,CE=2,而CEED=BEEF,
∴EF= ,∴EF=BE.(10分)
,∴EF=BE.(10分)
【解析】
试题分析:(1)由PA是圆的切线结合切割线定理得比例关系,求得PD,再由角相等得三角形相似:△PAC∽△CBA,从而求得AC的长;
(2)欲求证:“BE=EF”,可先分别求出它们的值,比较即可,求解时可结合圆中相交弦的乘积关系.
考点:与圆有关的比例线段,几何证明
点评:本题主要考查与圆有关的比例线段、圆中的切割线定理以及相似三角形的知识.

练习册系列答案
相关题目
 ,
, 有零点,则m的取值范围是
有零点,则m的取值范围是



 的倾斜角为135;命题q:直角坐标平面内的三点A(-1,-3),B(1,1),C(2,2)共线. 则下列判断正确的是
的倾斜角为135;命题q:直角坐标平面内的三点A(-1,-3),B(1,1),C(2,2)共线. 则下列判断正确的是 为假 B.
为假 B. 为真 C.
为真 C. 为真 D.
为真 D. 为真
为真 在点
在点 处的切线方程是( )
处的切线方程是( ) B.
B.
 D.
D.
 ,试比较
,试比较 与
与 的大小;
的大小; ,使得
,使得 对任意大于
对任意大于 的自然数
的自然数 都成立?若存在,试求出
都成立?若存在,试求出 的值并证明你的结论;若不存在,请说明理由.
的值并证明你的结论;若不存在,请说明理由.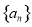 的前n项和为
的前n项和为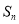 ,公差d≠0,且
,公差d≠0,且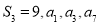 成等比数列.
成等比数列.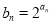 ,求数列{
,求数列{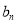 }的前n项和
}的前n项和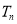 .
. ,若
,若 ,则
,则 .
.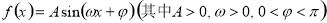 在
在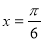 处取得最大值3,其相邻两条对称轴间的距离为
处取得最大值3,其相邻两条对称轴间的距离为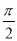 .
. 的解析式;
的解析式;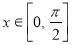 ,求
,求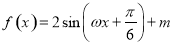 (其中
(其中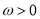 )的图像过点
)的图像过点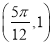 ,且其相邻两条对称轴之间的距离为
,且其相邻两条对称轴之间的距离为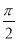 ,
,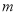 的值及
的值及 的单调递增区间;
的单调递增区间;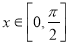 ,求
,求