题目内容
(本小题满分10分)(1)设 ,试比较
,试比较 与
与 的大小;
的大小;
(2)是否存在常数 ,使得
,使得 对任意大于
对任意大于 的自然数
的自然数 都成立?若存在,试求出
都成立?若存在,试求出 的值并证明你的结论;若不存在,请说明理由.
的值并证明你的结论;若不存在,请说明理由.
解:(1)设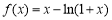 ,则
,则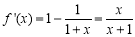 ,
,
当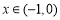 时,
时,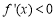 ,
,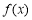 单调递减;
单调递减;
当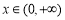 时,
时,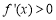 ,
,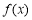 单调递增;
单调递增;
故函数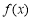 有最小值
有最小值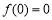 ,则
,则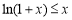 恒成立; 3分
恒成立; 3分
(2)取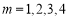 进行验算:
进行验算: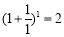 ,
,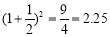 ,
,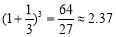 ,
,
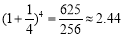 ,猜测:①
,猜测:①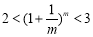 ,
,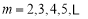 , 5分
, 5分
②存在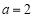 ,使得
,使得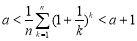 恒成立.
恒成立.
证明一:对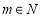 ,且
,且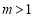 ,
,
有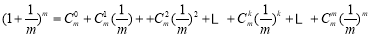
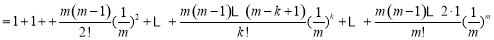
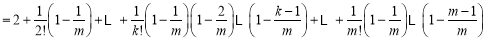
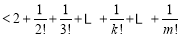
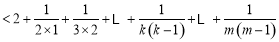
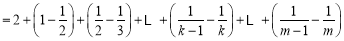
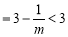 .
.
又因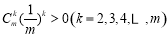 ,故
,故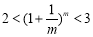 ,
,
从而有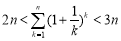 成立,即
成立,即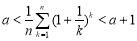 .
.
所以存在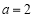 ,使得
,使得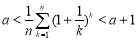 恒成立. 10分
恒成立. 10分
证明二:由(1)知:当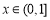 时,
时,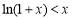 ,
,
设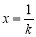 ,
,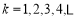 ,
,
则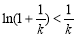 ,所以
,所以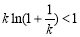 ,
,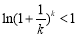 ,
,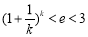 ,
,
当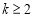 时,再由二项式定理得:
时,再由二项式定理得:
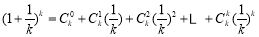
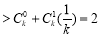 ,
,
即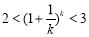 对任意大于
对任意大于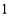 的自然数
的自然数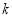 恒成立,
恒成立,
从而有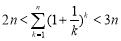 成立,即
成立,即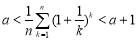 .
.
所以存在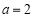 ,使得
,使得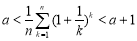 恒成立. 10分
恒成立. 10分
【解析】
试题分析:(1)复合函数求导求最值;(2)取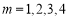 进行验算,得a=2,用二项式定理证明
进行验算,得a=2,用二项式定理证明
考点:复合函数的导数,二项式定理
点评:本题考查了复合函数的导数,二项式定理等综合应用,属难题.

练习册系列答案
相关题目
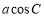 ,
,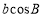 ,
,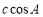 满足
满足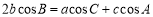 ,若
,若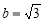 ,则
,则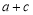 的最大值为
的最大值为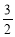 B.3 C.
B.3 C.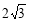 D.9
D.9 的焦点到它的准线的距离等于 .
的焦点到它的准线的距离等于 . 中,已知
中,已知 ,则
,则 __________
__________ 共焦点且过点
共焦点且过点 的双曲线方程是( )
的双曲线方程是( ) B.
B. C.
C. D.
D.

 ( )
( ) B.
B. C.
C. D.
D.