题目内容
焦点在x轴上的双曲线,它的两条渐近线的夹角为
,焦距为12,求此双曲线的方程及离心率.
| π |
| 3 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设焦点在x轴上的双曲线方程为
-
=1(a,b>0),由c=6,得到a2+b2=36.再由渐近线方程,运用夹角公式,得到a,b的方程,解得即可得到双曲线方程和离心率.
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:设焦点在x轴上的双曲线方程为
-
=1(a,b>0)
则渐近线方程为y=±
x,2c=12,即c=6,即有a2+b2=36.①
它的两条渐近线的夹角为
,则有tan
=|
|,
即有2ab=±
(a2-b2).②
由①②解得,a=3
,b=3或a=3,b=3
,
则双曲线的方程为
-
=1及离心率e=
=
,
或
-
=1,e=2.
| x2 |
| a2 |
| y2 |
| b2 |
则渐近线方程为y=±
| b |
| a |
它的两条渐近线的夹角为
| π |
| 3 |
| π |
| 3 |
| ||
1-
|
即有2ab=±
| 3 |
由①②解得,a=3
| 3 |
| 3 |
则双曲线的方程为
| x2 |
| 27 |
| y2 |
| 9 |
| c |
| a |
2
| ||
| 3 |
或
| x2 |
| 9 |
| y2 |
| 27 |
点评:本题考查双曲线的方程和性质,考查两直线的夹角公式,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知球的体积是
π,那么球的半径等于( )
| 32 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
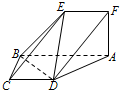 设平面ABCD⊥平面ABEF,AB∥CD,AB∥EF,∠BAF=∠ABC=90°,BC=CD=AF=EF=1,AB=2.
设平面ABCD⊥平面ABEF,AB∥CD,AB∥EF,∠BAF=∠ABC=90°,BC=CD=AF=EF=1,AB=2.