题目内容
已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)证明:
+
+…+
>
-
.
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)证明:
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| n |
| 2 |
| 1 |
| 2 |
考点:数列与不等式的综合,等比关系的确定
专题:证明题,等差数列与等比数列,不等式的解法及应用
分析:(1)易求a1=1,由题意得2an=Sn+n,2an+1=Sn+1+(n+1),两式相减后变形可得an+1+1=2(an+1),根据等比数列的定义可得结论,利用等比数列通项公式可求an+1,进而可得an;
(2)由于
=
>
=
-
,再由等差和等比数列求和公式,即可得证.
(2)由于
| an |
| an+1 |
| 2n-1 |
| 2n+1-1 |
| 2n-1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
解答:
(1)证明:n=1时,2a1=S1+1,
∴a1=1.
由题意得2an=Sn+n,2an+1=Sn+1+(n+1),
两式相减得2an+1-2an=an+1+1,即an+1=2an+1.
于是an+1+1=2(an+1),
又a1+1=2.
∴数列{an+1}为首项为2,公比为2的等比数列,
∴an+1=2•2n-1=2n,即an=2n-1;
(2)证明:由于
=
>
=
-
,
则有
+
+…+
>(
+
+…+
)-(
+
+…+
)
=
-
>
-
.
则原不等式成立.
∴a1=1.
由题意得2an=Sn+n,2an+1=Sn+1+(n+1),
两式相减得2an+1-2an=an+1+1,即an+1=2an+1.
于是an+1+1=2(an+1),
又a1+1=2.
∴数列{an+1}为首项为2,公比为2的等比数列,
∴an+1=2•2n-1=2n,即an=2n-1;
(2)证明:由于
| an |
| an+1 |
| 2n-1 |
| 2n+1-1 |
| 2n-1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
则有
| a1 |
| a2 |
| a2 |
| a3 |
| an |
| an+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n+1 |
=
| n |
| 2 |
| ||||
1-
|
| n |
| 2 |
| 1 |
| 2 |
则原不等式成立.
点评:本题考查数列的通项和前n项和间的关系,考查等比数列的通项公式和求和公式,考查数列不等式的证明方法:运用放缩法证明,考查推理能力,属于中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
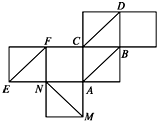 如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题:
如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题: 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…,以此类推,则第11行从左至右算第7个数字为
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…,以此类推,则第11行从左至右算第7个数字为