题目内容
(本题满分12分)
“坐标法”是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究图形的几何性质的方法,它是解析几何中是基本的研究方法. 请用坐标法证明下面问题:
已知圆O的方程是 ,点
,点 ,P、Q是圆O上异于A的两点.证明:弦PQ是圆O直径的充分必要条件是
,P、Q是圆O上异于A的两点.证明:弦PQ是圆O直径的充分必要条件是 .
.
详见解析.
【解析】
试题分析:若 ,即
,即 .设直线AP的方程是
.设直线AP的方程是 .与圆方程联立消去
.与圆方程联立消去 可得关于
可得关于 的一元二次方程.从而可求得
的一元二次方程.从而可求得 点坐标.同理可得点
点坐标.同理可得点 坐标.可得
坐标.可得 的坐标.根据坐标可得
的坐标.根据坐标可得 .从而可知
.从而可知 三点共线,即
三点共线,即 是圆
是圆 直径; 若弦
直径; 若弦 是圆的直径,可设
是圆的直径,可设 .根据向量数量积公式可得
.根据向量数量积公式可得 .
.
试题解析:证明: 充分性:若 ,即
,即
设直线AP的方程是 ,
,
代入 得
得 2分
2分
因为 ,所以
,所以 ,从而得
,从而得 4分
4分
因为 ,所以直线AQ的方程
,所以直线AQ的方程
以 代换点Q坐标中的
代换点Q坐标中的 ,得
,得 5分
5分
显然 ,即弦
,即弦 是圆的直径 6分
是圆的直径 6分
(Ⅱ)必要性:若弦 是圆的直径,设
是圆的直径,设 ,
,
 10分
10分
因为 ,所以
,所以 12分
12分
考点:1充分必要条件;2向量数量积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

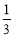
 C.
C. 是偶函数,其定义域为
是偶函数,其定义域为 ,且在
,且在 上是减函数,则
上是减函数,则 的大小关系是
的大小关系是 >
> B.
B. <
<


 D.
D.


 为等差数列,其前n项和为
为等差数列,其前n项和为 ,已知
,已知 ,
,
 ,若对任意
,若对任意 ,都有
,都有 成立,则k的值为
成立,则k的值为  的前
的前 项和
项和 当首项
当首项 和公差
和公差 变化时,若
变化时,若 是一个定值,则下列各数中为定值的是( )
是一个定值,则下列各数中为定值的是( )  B.
B. C.
C. D.
D.
 是等比数列,
是等比数列, ,则
,则 ____________.
____________. (y≠0) (B)
(y≠0) (B) (y≠0)
(y≠0) (y≠0) (D)
(y≠0) (D) (y≠0)
(y≠0) 的解集为
的解集为 ,则
,则 .
.