题目内容
10.已知cos($\frac{π}{2}$+α)=$\frac{1}{2}$,α∈(π,$\frac{3π}{2}$),则cosα=$-\frac{\sqrt{3}}{2}$.分析 由已知结合诱导公式求得sinα,再由平方关系求得cosα的值.
解答 解:由cos($\frac{π}{2}$+α)=$\frac{1}{2}$,得-sinα=$\frac{1}{2}$,
∴sinα=$-\frac{1}{2}$,
又α∈(π,$\frac{3π}{2}$),
∴cos$α=-\sqrt{1-si{n}^{2}α}=-\sqrt{1-(-\frac{1}{2})^{2}}=-\frac{\sqrt{3}}{2}$.
故答案为:$-\frac{\sqrt{3}}{2}$.
点评 本题考查运用诱导公式化简求值,考查了同角三角函数的基本关系式及三角函数的象限符号,是基础题.

练习册系列答案
相关题目
20.函数$y=\sqrt{{{log}_{\frac{3}{4}}}(3x-1)}$的定义域是( )
| A. | [1,3] | B. | $({-∞,\frac{1}{3}}]$ | C. | $({\frac{1}{3},\frac{2}{3}}]$ | D. | $({\frac{2}{3},+∞})$ |
1.设双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,点A是过F2且倾斜角为$\frac{π}{4}$的直线与双曲线的一个交点,若△F1F2A为等腰直角三角形,则双曲线的离心率为( )
| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\sqrt{3}+1$ | C. | $\frac{\sqrt{2}+1}{2}$ | D. | $\sqrt{2}+1$ |
18.已知命题p:?x∈R,x-1≥lgx,命题q:?x∈(0,π),sinx+$\frac{1}{sinx}$>2,则下列判断正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
5.如果直线x+ay+3=0与直线ax+4y+6=0互相平行,则实数a的值为( )
| A. | 2 | B. | -2 | C. | 0 | D. | -2或2 |
6.设扇形的周长为8,面积为4,则扇形的圆心角是(弧度)( )
| A. | 1 | B. | 2 | C. | 4 | D. | 1或2 |
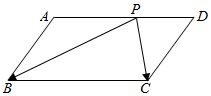 如图,在面积为4的平行四边形ABCD中,点P为直线AD上的动点,则$\overrightarrow{PB}•\overrightarrow{PC}+{\overrightarrow{BC}^2}$的最小值为4$\sqrt{3}$.
如图,在面积为4的平行四边形ABCD中,点P为直线AD上的动点,则$\overrightarrow{PB}•\overrightarrow{PC}+{\overrightarrow{BC}^2}$的最小值为4$\sqrt{3}$.